


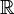 上的两个可积函数,作积分:
上的两个可积函数,作积分: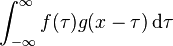 可以证明,关于几乎所有的
可以证明,关于几乎所有的  ,上述积分是存在的。这样,随着 x 的不同取值,这个积分就定义了一个新函数h(x),称为函数f 与g 的卷积,记为h(x) = (f * g)(x)。容易验证,(f * g)(x) = (g * f)(x),并且(f * g)(x) 仍为可积函数。这就是说,把卷积代替乘法,L1(R1) 空间是一个代数,甚至是巴拿赫代数。
,上述积分是存在的。这样,随着 x 的不同取值,这个积分就定义了一个新函数h(x),称为函数f 与g 的卷积,记为h(x) = (f * g)(x)。容易验证,(f * g)(x) = (g * f)(x),并且(f * g)(x) 仍为可积函数。这就是说,把卷积代替乘法,L1(R1) 空间是一个代数,甚至是巴拿赫代数。 ,它是其中一个函数翻转并平移后与另一个函数的乘积的积分,是一个对平移量的函数。
,它是其中一个函数翻转并平移后与另一个函数的乘积的积分,是一个对平移量的函数。 积分区间取决于f 与g 的定义域。
积分区间取决于f 与g 的定义域。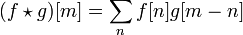 快速卷积算法当
快速卷积算法当 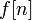 是有限长度 N ,需要约 N2 次运算。藉由一些快速算法可以降到 O(Nln N) 复杂度。
是有限长度 N ,需要约 N2 次运算。藉由一些快速算法可以降到 O(Nln N) 复杂度。 性质各种卷积算子都满足下列性质:
性质各种卷积算子都满足下列性质: 结合律
结合律 分配律
分配律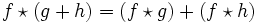 数乘结合律
数乘结合律 其中a为任意实数(或复数)。
其中a为任意实数(或复数)。 其中Df 表示f的微分,如果在离散域中则是指差分算子,包括前向差分与后向差分两种:
其中Df 表示f的微分,如果在离散域中则是指差分算子,包括前向差分与后向差分两种:

 其中
其中 表示f 的傅里叶变换。
表示f 的傅里叶变换。| 欢迎光临 电子技术论坛_中国专业的电子工程师学习交流社区-中电网技术论坛 (http://bbs.eccn.com/) | Powered by Discuz! 7.0.0 |