|
 
- UID
- 871057
- 性别
- 男
|

摘要:针对LED 动态照明的实现问题,本文提出一种基于两通道PWM 的调光调色方法。该方法通过分析PWM混光技术下的几何、光度、色度与电力约束条件,论证了两通道PWM 实现调光调色的确定性和局限性,建立了混合光的期望光度量、色度量与两通道占空比之间的定量计算模型。利用该方法对高、低色温两种白光LED 进行混光实验,模拟了自然光的照度和色温变化,实测值与理论值之间的平均误差分别是15 lx 和23 K.实验结果表明,此方法可以较好地实现预期光度、色度要求的光谱。
引 言
2002 年美国Brown 大学David Berson 等人在哺乳动物的视网膜上发现了第三种感光细胞,它主要在调节人体内分泌、控制生理节律等非视觉生物效应方面发挥功能。照明设计也从单一地考虑视觉功能逐步过渡到考虑视觉与非视觉双重功能上。研究表明,动态照明在治疗失眠、减轻飞机时差效应、提高工作效率等方面发挥作用。
为实现LED 的动态照明设计,需对光源的光色量进行实时地控制,调制出符合光生物学要求的光谱。
这里的光色量是光度量和色度量的合称。LED 常用的调光方法有模拟调光和PWM(Pulse Width Modulation)调光两种。前者是线性调节LED 电流,后者是使用开关电路以相对于人眼识别力足够高的频率来改变光输出的平均值。在调光过程中,防止色度量发生偏移相当重要。产生色偏的因素主要有两个:正向导通电流和P-N 结温度。模拟调光产生的色差取决于两者,PWM 则主要决定于后者。一般情况下PWM 产生较小的色差(白光LED因结温引起的色差不超过4SDCM),工程实践中多不考虑PWM调光产生的色差。
恒流驱动下的PWM 具有以下特点:改变LED 的占空比,光度量相应地线性改变而色度量保持恒定。光度量和色度量都是整数倍于方波周期时间内的平均值。PWM 也因具有较宽的调节范围,在工程实践中得到了广泛应用。
目前对PWM 调光调色的研究相对较少,此前尚缺乏一个利用PWM 同时控制光源光度量和色度量的量化计算方案。针对上述问题,提出了两通道PWM 调光调色的混光模型,建立了期望光色量与两通道占空比之间的一一映射。该算法能定量地调制出期望光度、色度要求的光谱,为LED 的动态照明设计提供了一个有效的实现方法。
1 方 法
1.1 两通道PWM 调光调色的确定性
理论上可以证明,通过对LED 进行混光,两通道PWM 的占空比与混合光的光色量之间存在确定的映射关系。这种确定性由PWM 混光技术下的几何、光度、色度约束条件共同决定。
1.1.1 几何约束条件
由色度学知识可知,混合光的色品坐标必在参与混光的两光源色品坐标连线上,具体位置取决于两种光源的混合比例。以此表示两通道PWM 混光的几何约束条件,用公式表示如下:

式中:xc、yc 和xw、yw 分别为参与混光的冷光源(高色温LED)和暖光源(低色温LED)在满电流、占空比为100%下的色坐标;xm、ym 为混合光的色坐标。
1.1.2 光度约束条件
改变驱动LED 的PWM 占空比,其色度量不变而光度量相应地线性变化,且光度量的比值等于占空比的比值。根据测试条件,光度量可以是光通量、照度、亮度或光强,色度量可以是色品坐标或相关色温。
若已知两光源的占空比,则混合光的光度量可结合叠加原理计算如下:

式中:Yc、Yw 分别为参与混光的冷光源和暖光源在满电流、占空比为100%下的光度量;Dc、Dw 分别为冷光源和暖光源的占空比;Ym 为混合光的光度量。这就是两通道PWM 混光的光度约束条件。
1.1.3 色度约束条件
根据加混色原理及CIE1931 色坐标计算方法,占空比分别为Dc、Dw 时两光源混光后的色坐标应满足:

式中: Rc = Y c / yc , Rw = Yw / yw 。实际上,由几何约束条件可知,当已知两光源的色品坐标和混合光的x坐标时,混合光的y 坐标是确定的,且是唯一的。故两通道PWM 混光的色度约束条件可简化为:

1.1.4 两通道PWM 调光调色的定量计算模型
在PWM 混光下,占空比是控制光色量的唯一因素。若期望的光度量为Ym,期望的色坐标为(xm,ym),则两通道占空比可结合光度、色度约束条件求得。若期望的色度量是相关色温,则需先将期望相关色温结合几何约束条件转换为期望色坐标。转换方法为:在CIE1931 色品图中做Tm 的等温线,把(xc,yc)和(xw,yw)的连线与此等温线的交点作为期望色坐标(xm,ym)。联立式(2)和式(4)并将其写成矩阵的形式如下:
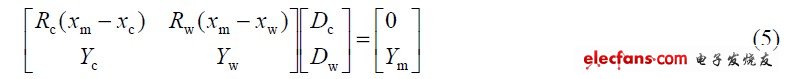
由线性代数知识可知,当 xc ≠ xw 且 yc ≠ yw 时方程组有唯一解。由此可知,给定期望色度、光度值下的占空比是确定的,且是唯一的。此时,计算占空比与计算混合光的光色量是可逆过程。
1.2 两通道PWM 调光调色的局限性
理论上,混合光色坐标xm 的取值范围为[xc,xw](设 xc 《 x w),混合光的光度量 Ym 的取值范围为[0, Yc + Y w ]。混合光色度量和光度量所有可能取值所围成的区域称作理论域。事实上,两通道PWM 的调光调色方法并不能实现理论域中的所有取值,而仅可实现部分特定的区域。可实现的区域称作可行域,可行域的边界主要由电力约束条件决定。
1.2.1 电力约束条件
从实际意义出发,两通道的占空比还应满足0 ≤ Dc ≤1 ,0 ≤ Dw ≤1 ,将式(5)解得的Dc、Dw代入该不等式,经化简后得到两通道PWM 混光下的电力约束条件如下:

上述电力约束条件可由图1 表示,图中x0=(Rc xc + Rwxw ) /(R c +Rw) ,是两种LED占空比之比为1:1 时混合光的色坐标x.图中所示的整个矩形区域就是两通道PWM 混光下的理论域,阴影部分即为可行域。若参与混光的两种LED 已选定,当利用式(5)计算实现期望光色量的占空比时,应首先判断期望值是否在可行域内。若在可行域中,则可利用两通道PWM 混光方法得到。
否则,应考虑更换参与混光的光源。

图1 两通道 PWM 调光调色的理论域和可行域
1.2.2 局限性的表征
为表征两通道PWM 调光调色的能力,定义可控比,它是可行域与理论域的比值,用公式表示为:
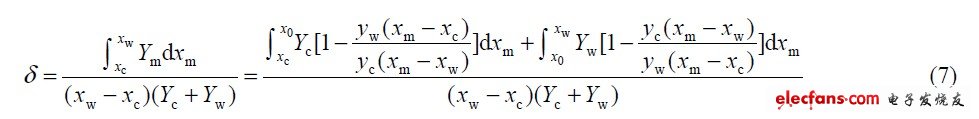
式中:δ 为可控比。将式(7)化简后可得:
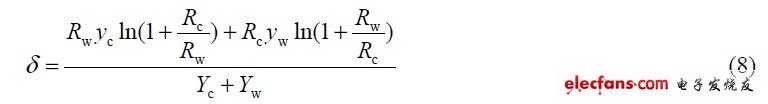
从上式可以看出,可控比由参与混光的两光源本身决定,与外在控制方法无关。可控比越大,说明PWM调控裕度越大,实现预期光度、色度值的概率越大。所以,可控比可作为光源组合选择优劣的评判标准。
从图1 中还可以看出:1) 混合光的色度量能且仅能在对应于x0 处取遍所有理论光度值;2) 若混合光的光度量不大于Yc、Yw 中的较小者,则可取遍所有理论色度值。所以要实现所有的色度值,Yc 和Yw 不应相差太大,且两者的较小值应与期望光度值中的最大值相当。同样实验表明,Rc 和Rw 的差值越小,则可控比就越大,两种LED 的利用率就越高。所以,在都能实现期望值的情况下,应选择Rc 和Rw 相差最小的光源组合。
2 实验与结果分析
根据P.R. Boyce、J.W. Beckstead、N.H. Eklund 等人实验提供的日光照度和色温变化曲线,选取26个时间关节点上的光色值,对从黎明到中午的自然光进行模拟。根据光色值的变化范围,选择了两种高显色性白光LED,LED 的光色电等基本参数如表1 所示。
根据两通道PWM 调光调色的局限性,计算期望光色值在理论域中的坐标值,如图2 所示。进而根据式(5)计算落在可行域内的各光色值的占空比。单片机把各时间点具备特定占空比的方波动态分配给相应的LED 驱动芯片。两种LED 均匀分布并用乳白玻璃将灯光混合,用检测设备实时测量其混合光的光色量。
检测仪器选用SUV3000 紫外可见光谱辐射分析仪,测量过程在标准暗室中进行。测量结果如图3 所示。
实测照度值与期望照度值的平均误差为15 lx,实测色温值与期望色温值平均误差为23 K.
表1 实验用 LED 的基本参数

实验过程中,实测值与理论值存在一定的误差,但总体上还是得到了很好的匹配。误差主要来自以下几个方面:1) 随着实验过程的进行,LED 芯片的结温不断升高。结温的改变会引起其光度量和色度量的变化。2) 驱动LED 芯片的PWM 波形并非理想的方波。即使在同一开关状态下,电流也并非保持恒定。
而驱动电流的变化则会导致LED 光度量和色度量的变化。占空比越小,这种情况引起的误差就越大。
3) LED 个体性差异。即使是同一型号,同一批次的LED,其光度量和色度量也会不同,特别是两者的动态特性。而在实验中认为同一种LED 具有相同的光色电参数和动态特性。4) 检测仪器的系统误差以及操作过程中的随机误差。
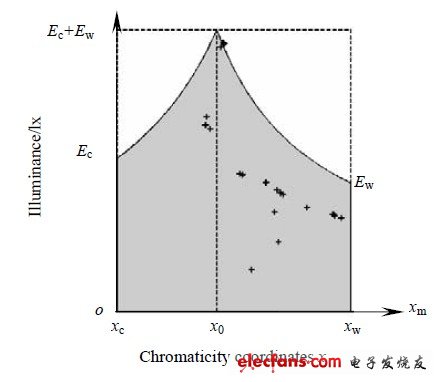
图2 实验光色值在理论域中的分布。
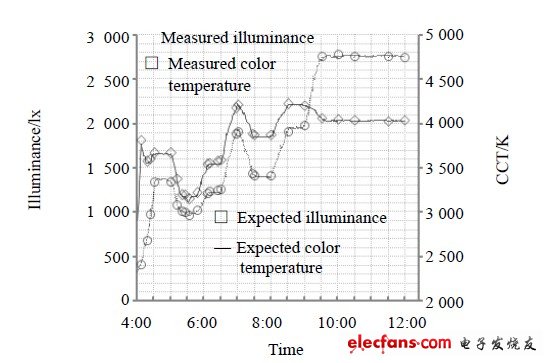
图 3 模拟从黎明到中午自然光的照度和色温变化。
3 结 论
本研究提出了一种新型的基于PWM 的调光调色方法,建立了关于期望光色量和两通道占空比的一一映射模型,可以准确的实现预期光度和色度要求的光谱,为LED 的动态照明技术提供了理论依据和实现方法。另外,该调光调色方法在LED 背光领域亦具有潜在的应用前景。 |
|