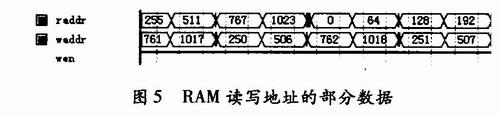
 图1中的地址产生单元作为系统的控制核心，不仅要生成每一级的RAM读写地址，还要产生RAM写使能信号、输出有效信号以及4点蝶形运算单元和旋转因子产生单元的启动信号，由于时序电路还需要考虑器件延时，例如上文提到的4点蝶形运算输出比输入延时6个时钟，以及RAM存取数据输出比输入延时1个时钟，这些都需要在控制核心中考虑到。
1.4旋转因子产生
对于1 024点FFT蝶形运算，需要1 024个旋转角度（即2π的1 024等份），其中第一级不需要复乘运算，第6级只是将数据进行整序没有运算单元，其他4级都需要旋转因子。本设计采用将旋转因子预置于ROM中，通过查找表方法得出每一级运算的所需的旋转因子。根据旋转因子的可约性，后几级运算所需的旋转因子都可以在第一级运算的旋转因子中找到，因此无需另外存储。旋转因子在ROM中的存储规律是：旋转因子相位角p处存储旋转因子W=*****.定义一个10 bit的计数器count[9：0]，则第2、3、4、5级ROM的相位角规律按照Verilog语法可表示
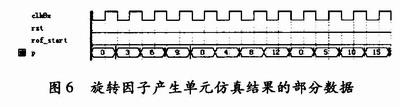
为了节省资源，本设计只在ROM单元中存储了前256个旋转因子数据，即第一象限因子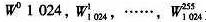 其余象限的因子可通过象限转换后得到，这样就大大节省了存储单元的硬件资源。图6为旋转因子产生单元在QuartusⅡ环境中仿真结果的部分数据。
2系统仿真结果
输入数据为s=1 024×cos（2π×f_in×t），其中f_in=50 M，Fs=80 MHz，n=40，t=0：1/Fs：（n-1）/Fs，利用QuartusⅡ软件对系统在100 MHz的时钟环境下进行了仿真，将仿真输出结果转换成tbl文件并利用Matlab软件读取后，得到如图7所示的频谱数据图（实部数据部分）。
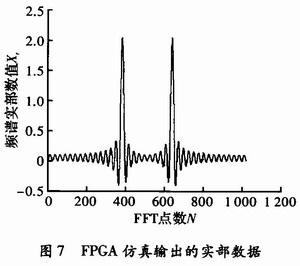
图8所示为Maflab自带FFT函数对于输入相同1 024点数据的FFT计算结果（同样为实部数据部分）。
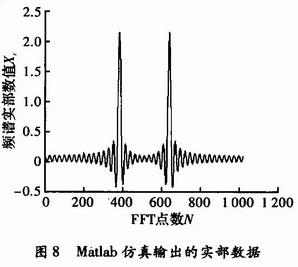
通过比较可以看到，本设计的仿真结果与Matlab的仿真结果基本一致，可以正确高效地计算出1 024点FFT数据。
3结束语
本设计全部由Verilog HDL语言实现，采用自顶向下的设计方法，完成了一种基于FPGA的1 024点16位FFT算法，共需要5级运算，每级需要计算256个蝶形。提出了将蝶形运算先进行前一级的蝶形加减运算，再进行本级的与旋转因子复乘运算的结构。由前所述，平均每个蝶形运算需要4个时钟周期，所以理论上完成1 024点FFT的总时钟周期为N=256×4×5=5 120；假设使用的时钟为100MHz，那么将耗时T=5 120×（1/100）=51.2μs，这与仿真结果51.32μs基本一致。 |
