|
 
- UID
- 1023230
|

本文中,将以MAX5891 作为测量和规格说明的特例。但所介绍的参数和测量方法可以用于其他的差分输出、电流模式DAC。
线性参数说明
定义数据转换器线性精度主要有两个参数:积分(INL)和差分(DNL)非线性。INL是输出传输函数和理想直线之间的偏差;DNL是转换器输出步长相对于理想步长的误差。
可以采用两种方法之一对INL进行定义:(1)端点INL或(2)最佳拟合INL。端点INL是采用DAC传输函数端点测得的实际值计算转换器的线性度;最佳拟合INL则是计算传输函数的斜率获得INL的峰值。

图1a. 端点积分非线性误差

图1b. 最佳拟合积分非线性误差
图1a和图1b以图形的形式显示了两种测试方法与给定传输函数之间的关系。注意,两种情况中,DAC传输函数曲线的数值和形状都一样。还要注意,图1a的端点线性度有较大的正INL,而没有负误差。
采用图1b所示的最佳拟合方法,将部分正误差转移到直线的负侧,以降低报告的最大INL。注意,线性度误差总量和直线计算结果相同。
DNL定义理解起来要难一些,确定最低有效位(LSB)的权值会影响DNL。DAC中需要考虑DNL没有小于-1 LSB的编码。小于这一电平的DNL误差表明器件是非单调的。当输出不随输入码增大而减小时,或者输出不随输入码减小而增大时,DAC是单调的。图2解释了正、负DNL误差,澄清了单调的概念。
测量线性度所采用的方法需要考虑待*估DAC的体系结构。优先选择将电流模式DAC输出转换为电压,因为这样可以使用电压表而不是电流表。普通的万用表在测量电压时分辨率要高于电流测量。电流源的配置决定了需要测量多少位编码才能对器件性能进行精确的*估。

图2. DNL误差实例
有很多方法可以将电流(I)转换为电压(V),主要取决于几种因素。首先考虑使用万用表进行测量,能够得到的最高分辨率决定了精确测量的最小LSB权重。推荐LSB权重与仪表分辨率的比是100比1;仪表应能够测量LSB的1/100。
待测DAC的输出额定容限也影响了如何进行I至V的转换。电流模式DAC输出容限是指器件在输出上能够承受多大的电压而不会对性能有影响。增大负载电阻会提高电压摆幅和LSB的大小,但是容限限制了最大负载。
替代简单的电阻转换的方法是使用虚拟地配置的运算放大器,如图3所示。由于DAC输出电压保持为零,这种配置的优势是能够提高LSB的大小,明显高于容限限制。然而,放大器容限和线性度以及热梯度会影响测量。同样的,需要两个匹配放大器来测量差分输出器件。
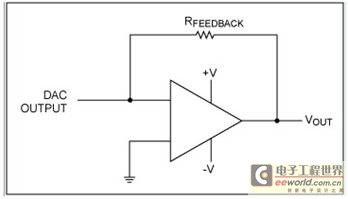
图3. 虚拟地的I至V转换
测量线性度时需要考虑的另一因素是待*估DAC的分辨率。器件分辨率越高,LSB越小。考虑MAX5891 (16位)、MAX5890 (14位)、MAX5889 (12位)器件。每一器件的满量程输出为20mA。使用50Ω负载时,相应的LSB大小为15.25?V、61.04?V和244.2?V。LSB越小,万用表需要的精度和分辨率就越高。
考虑到DAC的分辨率,还应该确定需要多少位编码才能精确地测量器件性能。16位器件有65,536个可能的输入编码,12位器件有4,096个。由于不可能人工测量所有这些编码,因此,常用的方法是测量编码子集。少量的编码减少了采集数据所需要的时间,并且能够提供非常精确的结果。掌握器件的体系结构有助于选择某一器件的最佳编码。
测量电流输出器件的线性度时,温度效应比较明显。输出负载电阻的功耗导致发热,从而改变了电阻值(除非采用的电阻具有0ppm温度系数)。解决这一问题的方法是转换输入编码,有效地对负载功耗进行平均。
这里采用的方法非常适合自动测量,因为它能够减小所有编码的延迟时间。测量每一编码及其补码,例如0x4800,然后是0xB7FF。通过测量每一编码及其补码,负载平均功率保持固定,这是因为采用了从零到满量程递增的方式来测量最高有效位(MSB)输入。由于在量程中部测量LSB,该方法不太适合,因为功率的变化相当小。
测量说明
以下是Maxim开发的几种器件所采用的线性度测量方法。MAX5873 、MAX5875 、MAX5885、MAX5888 MAX5891、MAX5895 和MAX5898 /都采用了该方法进行测量。在最初设计*估和产品测试时进行了实验室测量。虽然下面实例针对MAX5891,该方法也可以用于其他器件。
MAX5891采用了5-4-3-4分段结构。分段是指将一个16位器件有效地分成四个单独的DAC,一个5位、一个4位、一个3位和第二个4位器件。5个MSB含有31个(25 - 1)等权重电流源,对于5位分辨率,每个输入编码采用一个等权重电流源。下一个4位使用15个源,再下一个3位使用7个。4个LSB是二进制权重电流源,每个低位比特等于前一比特值的一半。
电流源的总数57 (31 + 15 + 7 + 4)加上满幅值和零值,确定了测量MAX5891线性度所需的最少编码数。59次测量支持重新构建完整的DAC输出传输函数。一旦确定了传输函数,即可计算线性度。该方法虽然缩短了测试时间,但降低了测量精度。表1列出了推荐的MAX5891编码组。
表1. 5-4-3-4体系结构16位编码组
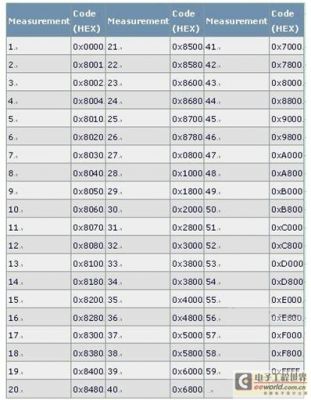
MAX5890和其他Maxim 14位器件使用5-4-3-2分段体系结构,14位体系结构的编码组如表2所示。MAX5889和其他Maxim 12位器件使用5-4-3体系结构,12位体系结构的编码组如表3所示。
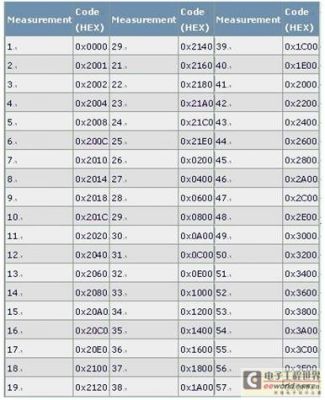
表2. 5-4-3-2体系结构的14位编码组
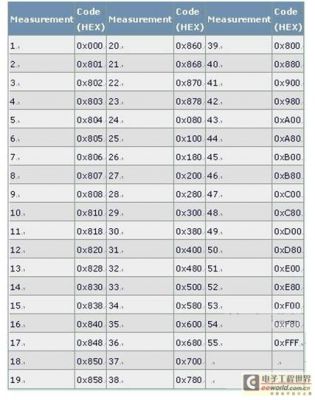
表3. 5-4-3体系结构的12位编码组
定义了编码组后,必须解决采集测量点的问题。适合这类测量的万用表是Agilent? 3458,分辨率高达8.5位。该表连接在MAX5891的OUTP和OUTN端之间,输出端以50Ω负载接地。当DAC设置为20mA满量程电流时,万用表输入得到的电压摆幅是±1V。
万用表量程设置为固定的1.2V,使用最大分辨率,得到10nV最小测量结果。切换表的量程会增大测量值的增益误差;因此,使用单电压量程可以避免其他的误差源。由于需要锁存数字输入,MAX5891还需要时钟信号。一旦连接好了万用表、时钟源、电源和数字输入控制,就可以采集线性度测量点。
采集所有测量点后,需要画出重建后的DAC输出传输函数。由于对每一电流源都进行了测量,很容易产生对应于所有编码的传输函数。例如,考虑器件的4个LSB。我们测量编码0x8000、0x8001、0x8002、0x8004和0x8008。对于编码0x8000,LSB计算的基准是DAC量程中部。LSB权重是在0x8001测得的电压值减去在0x8000测得的电压值。
在0x8001和0x8780之间测量的所有编码采用相同的公式。0x0800到0xF800的其他点是MSB电流源,以编码0x0000为基准进行计算。考虑编码0x4F31作为各种电流相加的例子。
首先,我们需要确定哪一测量点什么时候相加能够等于实例编码。0x4800是小于目标编码的最大MSB。从0x4F31中减去0x4800后的余数为0x0331。编码0x0300是可以减掉的次最大编码(0x8300 - 0x8000),随后是0x0030 (0x8030 - 0x8000),最后是0x0001 (0x8001 - 0x8000)。
因此,可以采用下面的等式来表示编码0x4F31的电压值:
[V(0x4800) - V(0x0000)] + [V(0x8300) - V(0x8000)] + [V(0x8030) - V(0x8000)] + [V(0x8001) - V(0x8000)](公式1)
使用相似的等式,可以计算任意给定输入编码的电压值。利用MATLAB?或Excel?软件等工具可以很容易地计算所有编码的电压,重建全部的DAC传输。
一旦建立了传输函数,就可以计算线性度。第一步是根据传输函数的端点计算LSB的电压值(端点法)。
VLSB = [V(0xFFFF) - V(0x0000)]/[2N - 1](公式2)
其中
N是器件分辨率 (16、14或者12位)
V(0x0000)是测得的DAC零标输出电压。
V(0xFFFF)是测得的DAC满幅输出电压。
采用下面的等式来计算任意给定编码的INL:
INLCODE(LSB) = [VCODE - (CODE × VLSB)]/VLSB(公式3)
其中
CODE是要计算的数字编码。
VLSB是公式2中计算的电压值。
VCODE是计算的DAC输出电压值。
下面的等式用于计算任意给定编码的DNL:
DNLCODE(LSBs) = [VCODE - VCode-1 - VLSB]/VLSB(公式4)
其中
CODE是要计算的数字编码。
VCODE是针对CODE计算的DAC输出电压值。
VCODE-1是针对CODE - 1计算的DAC输出电压值。
VLSB是公式2中计算的电压值。
以下举例说明利用MATLAB脚本计算MAX5889、MAX5890和MAX5891的线性度。每次计算都得到最小和最大DNL和INL误差编码和误差值。实例还为所有编码画出了传输函数,得到INL和DNL。要求用户输入前面表格中所列出编码的电压测量值。必须按照所列顺序输入数值。
计算16位线性度的MATLAB脚本
function Lin16(Measurements)
%Calculate INL and DNL of a 16-bit device with a 5-4-3-4 segmentation architecture
% DacCodes is the range of possible input data to the 16-bit DAC
DacCodes=[0:65535]’;
%VOUT for each code is calculated from the measured points
%create a VOUT variable and fill it with zeros
VOUT=zeros(size(DacCodes));
%The first measurement is the zero-scale point, or code (0x0000)
ZS=Measurements(1);
VOUT(1)=ZS;
%The last measurement is the full-scale point, or code (0xFFFF)
FS=Measurements(length(Measurements));
VOUT(65536)=FS;
%Midscale is stored at position 43 of the input data array
MS=Measurements(43);
%The device has four segmentation levels
Segments=4;
%The decimal values for the LSB codes are 1, 2, 4 and 8
Seg1Codes=[1;2;4;8];
%The voltages for the LSBs are in positions 2-5 of the input array
for i=1:4
Seg1V(i)=Measurements(i+1)-MS;
end
%The second level of segmentation is controlled with input codes 16 through
%112 in steps of 16. Create the code array and fill the measurements for
%this segmentation level
Seg2Codes=[16:16:16*7]’;
for i=1:7
Seg2V(i)=Measurements(i+5)-MS;
end
%Segmentation level 3 uses input codes 128 through 1920 in steps of 128.
%Create the code array and fill the measurements array.
Seg3Codes=[128:128:128*(2^4-1)]’;
for i=1:15
Seg3V(i)=Measurements(i+12)-MS;
end
%Segmentation level 3 uses input codes 2048 through 63,488 in steps of 2048.
%Create the code array and fill the measurements array.
Seg4Codes=[2048:2048:2048*(2^5-1)]’;
for i=1:31
Seg4V(i)=Measurements(i+27)-ZS;
end
%The endpoints have been defined, now fill in the voltages for the
%remaining points of the DAC transfer function.
for i = 2:65535
targetcode=i-1;
VOUT(i)=ZS;
for s=31:-1:1
if Seg4Codes(s)<=targetcode
targetcode=targetcode-Seg4Codes(s);
VOUT(i)=VOUT(i)+Seg4V(s);
s=0;
end
end
for s=15:-1:1
if Seg3Codes(s)<=targetcode
targetcode=targetcode-Seg3Codes(s);
VOUT(i)=VOUT(i)+Seg3V(s);
s=0;
end
if targetcode==0
s=0;
end
end
for s=7:-1:1
if Seg2Codes(s)<=targetcode
targetcode=targetcode-Seg2Codes(s);
VOUT(i)=VOUT(i)+Seg2V(s);
s=0;
end
if targetcode==0
s=0;
end
end
if targetcode==0
s=0;
end
for s=4:-1:1
if Seg1Codes(s)<=targetcode
targetcode=targetcode-Seg1Codes(s);
VOUT(i)=VOUT(i)+Seg1V(s);
end
end
end
%Plot the transfer function
figure(1)
plot(DacCodes, VOUT);
xlabel(‘DAC Input Code’);
ylabel(‘Measured Voltage’);
axis([0 65536 -1.1 1.1]);
title(‘DAC Transfer Function’);
set(gca,’XTick’,0:16384:65536)
%Calculate the linearity
LSB=(max(VOUT)-min(VOUT))/65535;
INL(1)=0;
DNL(1)=0;
for i=2:65536
INL(i)=(VOUT(i)-(VOUT(1)+(i-1)*LSB))/LSB;
DNL(i)=(VOUT(i)-VOUT(i-1)-LSB)/LSB;
end
%Plot INL
figure(2)
plot(DacCodes, INL);
title(‘DAC Integral Linearity’);
xlabel(‘DAC Input Code’);
ylabel(‘INL (LSBs)’);
axis([0 65536 min(INL)*1.1 max(INL)*1.1]);
set(gca,’XTick’,0:16384:65536)
%Plot DNL
figure(3)
plot(DacCodes, DNL);
title(‘DAC Differential Linearity’);
xlabel(‘DAC Input Code’);
ylabel(‘DNL (LSBs)’);
axis([0 65536 min(DNL)*1.1 max(DNL)*1.1]);
set(gca,’XTick’,0:16384:65536)
txtstr=sprintf(‘INL MAX = %f’, max(INL));
disp (txtstr);
txtstr=sprintf(‘INL MIN = %f’, min(INL));
disp (txtstr);
txtstr=sprintf(‘DNL MAX = %f’, max(DNL));
disp (txtstr);
txtstr=sprintf(‘DNL MIN = %f’, min(DNL));
disp (txtstr);
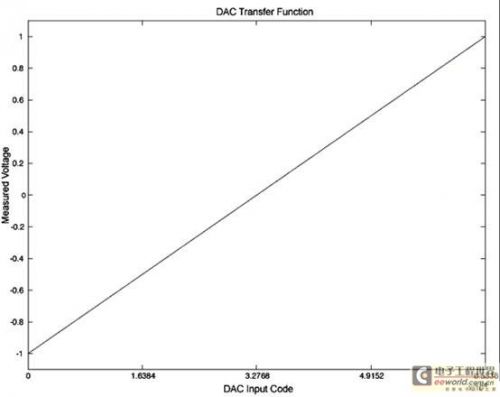
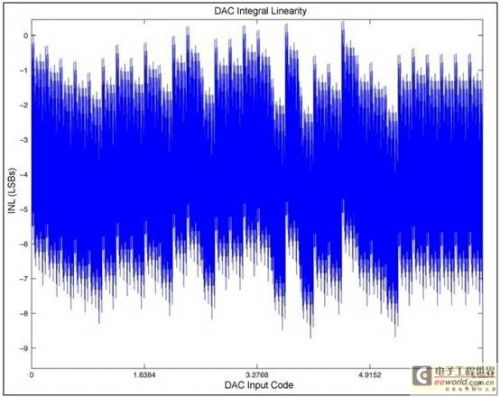
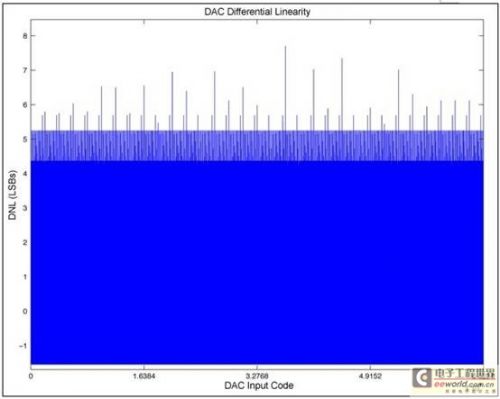
16位脚本产生的曲线 |
|


