2.3 计算机实现的理论研究
在程序中,滤波反投影算法的步骤为:
- 投影数据采集
- 对投影数据做FFT变换
- 滤波
- 反投影数据
- 逆FFT变换
等式(2.8)不能以它现有形式直接实现,只要考虑公式(2.10)的解释,就很容易理解这一点。基于傅里叶变换的特性,我们知道在傅里叶域中两个函数相乘等价于两个相应空间域函数的卷积。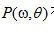 在空间域中的对应函数是被测平行投影 在空间域中的对应函数是被测平行投影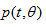 。对应滤波函数 。对应滤波函数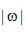 的空间领域(或冲激响应) 的空间领域(或冲激响应)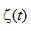 ,就是该函数的傅里叶反变换, ,就是该函数的傅里叶反变换,
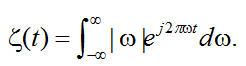 (2.12) (2.12)
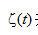 并不存在。必须研究一个代替方法。一个这样的方法是把有限带宽函数引入公式中。例如在上式中设置t=0,让我们考虑 并不存在。必须研究一个代替方法。一个这样的方法是把有限带宽函数引入公式中。例如在上式中设置t=0,让我们考虑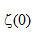 的值。 的值。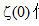 代表在曲线 代表在曲线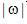 下面的面积。当 下面的面积。当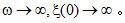 。因此,等式(2.8)不能以它现有形式实现。必须研究一个代替方法。一个这样的方法是把有限带宽函数引入公式中。 。因此,等式(2.8)不能以它现有形式实现。必须研究一个代替方法。一个这样的方法是把有限带宽函数引入公式中。
假设投影的傅里叶变换是有限带宽的。换句话说,在频率间隔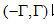 以外能量为0.在这个假设下,等式(2.10)可以按下面形式表示: 以外能量为0.在这个假设下,等式(2.10)可以按下面形式表示:
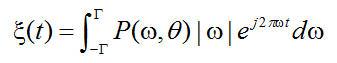 (2.13) (2.13)
等式(2.13)指出,要计算滤波的投影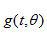 ,只需要进行投影 ,只需要进行投影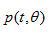 的傅里叶变换以得到 的傅里叶变换以得到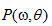 ,在 ,在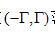 范围内乘以 范围内乘以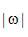 ,并进行傅里叶反变换。不幸的是,有两个因素使这个看似简单的问题变得复杂:被截断的滤波核的离散化以及环状卷积的性质。要彻底理解滤波核问题,让我们首先在空间域中推导理想滤波核。为保证无混叠采样,投影带宽T必须满足Nyquist(奈奎斯特)采样准则: ,并进行傅里叶反变换。不幸的是,有两个因素使这个看似简单的问题变得复杂:被截断的滤波核的离散化以及环状卷积的性质。要彻底理解滤波核问题,让我们首先在空间域中推导理想滤波核。为保证无混叠采样,投影带宽T必须满足Nyquist(奈奎斯特)采样准则:
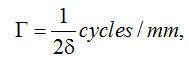 (2.14) (2.14)
其中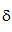 是投影采样间隔(单位为 是投影采样间隔(单位为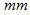 )。在该条件下,初始的斜变函数 )。在该条件下,初始的斜变函数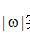 实际上是与窗函数 实际上是与窗函数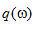 相乘: 相乘:
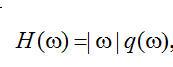 (2.15) (2.15)
其中
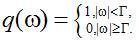
滤波函数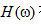 在图2.1中描绘。现在,滤波器冲激响应可以描述如下 在图2.1中描绘。现在,滤波器冲激响应可以描述如下
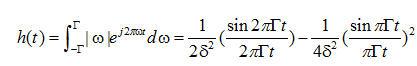 . (2.16) . (2.16)
注意由于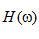 的 的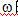 的一个实偶函数,相应的冲激响应 的一个实偶函数,相应的冲激响应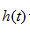 也是t的一个实偶函数。 也是t的一个实偶函数。
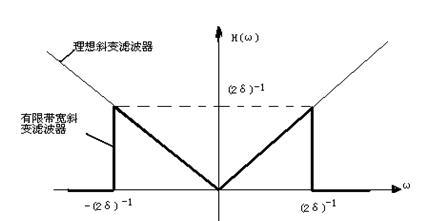
图2.1 有限带宽斜变滤波器的频率表示
注意,投影以间隔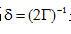 采样。根据卷积理论,等式(2.9)可以写为 采样。根据卷积理论,等式(2.9)可以写为
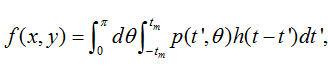 (2.17) (2.17)
其中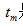 是满足条件 是满足条件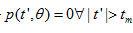 的 的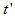 值。这里,我们利用被扫描物体具有有限空间紧支集这一事实。在滤波投影的离散实现时,我们只对在 值。这里,我们利用被扫描物体具有有限空间紧支集这一事实。在滤波投影的离散实现时,我们只对在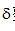 整数倍处的滤波数值感兴趣。把 整数倍处的滤波数值感兴趣。把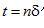 代入等式(2.16)中,得到 代入等式(2.16)中,得到
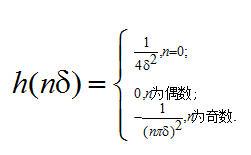 (2.18) (2.18)
滤波函数的冲激响应在图2.2中画出。在该图中,我们设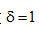 。如果用 。如果用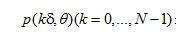 表示在角度 表示在角度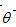 下投影的离散采样,等式(2.10)中描述的滤波投影可以表达为一个空间域卷积: 下投影的离散采样,等式(2.10)中描述的滤波投影可以表达为一个空间域卷积:
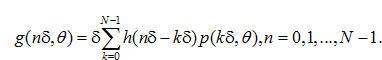 (2.19) (2.19)
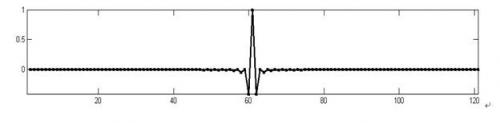
图2.2 斜边滤波器的冲激响应
这里,我们利用了每个投影在空间上具有有限紧支集的事实。即在下标范围以外,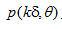 为0.这意味着,要确定 为0.这意味着,要确定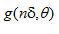 ,我们只需利用在范围 ,我们只需利用在范围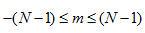 内的 内的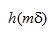 。 。
尽管等式(2.19)的离散卷积实现可以直接得到被滤波的投影,当N很大时,往往在频率域中执行运算效率更高[使用快速傅里叶变换(FFT)运算]。对于目前一台典型的CT扫描机,一次单独投影的采样数N接近1000.因此,我们希望得到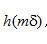 序列的频率域形式。在有限范围内 序列的频率域形式。在有限范围内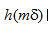 的离散傅里叶变换 的离散傅里叶变换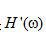 与等式(2.15)描述的 与等式(2.15)描述的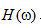 不同,如图2.3所示。二者之间主要差别是直流成分。尽管差相当小,它对重建图像CT数准确度的影响不能忽略。 不同,如图2.3所示。二者之间主要差别是直流成分。尽管差相当小,它对重建图像CT数准确度的影响不能忽略。
现在我们考虑循环卷积[9]的问题。等式(2.10)中描述的原始滤波运算需要一个非周期性的卷积。当这个运算在频率域中执行时,只能是周期性或循环卷积。如果直接实线前面所述的运算序列,可能产生干涉伪像。这就是所谓的卷绕(warp-around)效应,或者周期间干涉。为了避免伪像,需要在傅里叶变换和滤波运算之前为每个投影填补足够数量的零。零的最少数目必须等于初始投影采样数减1(即N-1)。
图2.3中所示斜变滤波器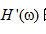 的特性表明,相对于低频成分, 的特性表明,相对于低频成分,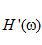 更突出强调高频成分。事实上,斜变滤波器表现有些好像微分运算符。因此,可以把滤波运算想象为一个反卷积过程,去掉了反投影产生的模糊。 更突出强调高频成分。事实上,斜变滤波器表现有些好像微分运算符。因此,可以把滤波运算想象为一个反卷积过程,去掉了反投影产生的模糊。
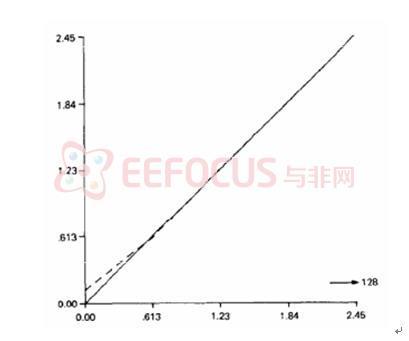
图2.3 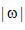 函数(实线)和有限带宽斜变滤波器傅里叶变换(虚线)的比较 函数(实线)和有限带宽斜变滤波器傅里叶变换(虚线)的比较
在等式(2.15)中,我们采用了一个简单的矩形窗函数来限制滤波核。可以另外修改窗函数,以改变滤波器的频率响应。实际应用中,窗函数经常被作为一个工具,用来修改重建图像的噪声特性,以实现空间分辨率和图像噪声之间的折中。
在许多用于数值计算和图像的高级语言软件系统中,如Matlab(The MathWorks,Natick,MA)或IDL(Research Systems,Inc,Boulder,CO),矢量或矩阵可以直接表示成变量。还可以针对矢量定义不同运算符。在这样的环境中,平行反投影的实现变得相当容易。对于每个被测投影(在数据预处理或预调理后),投影被填补足够多的0以避免“周期间”干扰。对补零后的投影进行傅里叶变换,并且被变换的投影乘以一个滤波函数[10]。然后,对结果进行傅里叶反变换,得到一个被滤波的投影。该投影被反投影(通过“像素驱动”或“射线驱动”)到图像矩阵。为了提高空间分辨率,滤波投影经常在反投影过程之前进行预插值。在投影数据集合中对每次投影重复整个过程。图2.4显示一个流程图,描述了对于平行束投影[11]的重建过程。
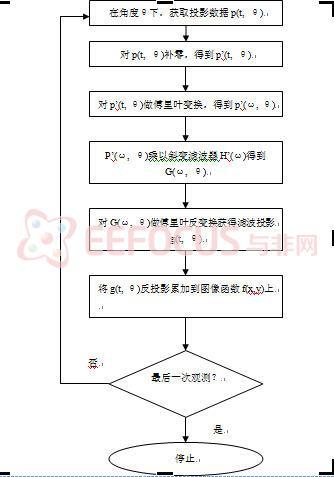
图2.4 平行投影重建过程的流程图
2.4 目标重建过程
医用CT的典型图像矩阵512×512。对于50cm重建FOV,每个像素尺寸大约1mm。根据Nyquist采样理论,这样的采样密度所支持的最高频率成分是5lp/cm(线对/厘米)。如果想检查具有更高空间辨率成分的解剖结构,图像像素间的采样距离必须减小。这可以通过增大重建图像矩阵尺寸或减小重建FOV来实现。增大的图像尺寸不仅影响重建速度(因为要被重建像素数与矩阵尺寸成平方关系),而且增加存储量。
另一可选方案是减少重建FOV。因为大多数高分辨率应用只需要检查很小一个区域(如内听管或脊椎骨),缩小的FOV不会产生限制。考虑到重建被定位到一个较小区域这个事实,该方法经常被称为“目标”或“缩放”重建。
目标重建过程类似于全FOV重建。一旦得到一个滤波投影(滤波过程和全FOV过程一致),反投影将缩小的FOV映射到投影上去。例如,假设对一个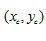 重建FOV进行像素驱动反投影,该FOV中心相对于系统旋转中心的坐标 重建FOV进行像素驱动反投影,该FOV中心相对于系统旋转中心的坐标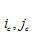 。进一步假设图像矩阵尺寸为n×n,图像矩阵中心标记为 。进一步假设图像矩阵尺寸为n×n,图像矩阵中心标记为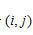 。一个位于 。一个位于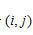 的图像像素可以映射到中心为旋转中心的原始坐标系统中的一个点,根据以下等式: 的图像像素可以映射到中心为旋转中心的原始坐标系统中的一个点,根据以下等式:
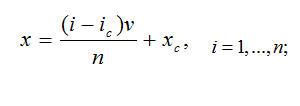 (2.20) (2.20)
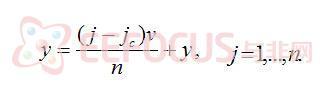 (2.21) (2.21)
由于知道如何对位于(x.y)的点进行全FOV重建的反投影,滤波投影可以按照类似于全FOV重建的方式定位、插值,并加到重建图像中。
第三章 Matlab下模型的建立
3.1 Simulink简介
由于Matlab具有语法筒单、易学、好写以及有强大的运算及绘图能力和强大且多样化的各种工具箱可供使用的优点,我们决定在Matlab下面进行模型的建立,对比m文件和simulink的优缺点,我们采用较为直观的Simulink仿真形式进行仿真。
Simulink是一个用来对动态系统进行建模、仿真和分析的软件包,它支持连续、离散及两者混合的线性和非线性系统,也支持具有多种采样频率的系统。在Simulink环境中,利用鼠标就可以在模型窗口中直观地“画”出系统模型,然后直接进行仿真。它为用户提供了方框图进行建模的图形接口,采用这种结构画模型就像你用手和纸来画一样容易。它与传统的仿真软件包微分方程和差分方程建模相比,具有更直观、方便、灵活的优点。Simulink包含有SINKS(输入方式)、SOURCE(输入源)、LINEAR(线性环节)、NONLINEAR(非线性环节)、CONNECTIONS(连接与接口)和EXTRA(其他环节)子模型库,而且每个子模型库中包含有相应的功能模块。用户也可以定制和创建用户自己的模块。
|