1.3 CT图像重建技术概述
1.3.1 CT图像重建的简介
我们试图重建的物体可被看作是某种函数的二维分布。对于CT，该函数代表物体线性衰减系数。关于断层重建问题的描述，我们可以假设采集了一组测量结果，每个测量结果代表沿着特定的射线路径，物体衰减系数的累加或线积分。这些测量结果是在不同角度和到旋转中心的不同距离上获取的。为避免数据采样的冗余，我们假设测量按以下次序进行。首先沿着彼此平行且等间距的路径进行一组测量。这些测量结果构成一次“观测”或一组“投影”。在略微改变的角度下重复同样的测量。持续该过程直到覆盖整个360°（理论上仅有180°平行投影是必要的）。在整个过程中，相邻两次观测之间的角度增量保持不变，并且被扫描物体在同一位置固定不动。CT重建的问题就是，我们如何基于这些测量结果来估计被扫描物体的衰减系数分布。
CT图像重建问题是一个有趣而复杂的课题。它的公示表达可以追溯到1917年，当时Radon(雷登）[2]首先找到了从函数线积分重建该函数的求解方法。随着20世纪70年代后期和80年代早期临床实用CT扫描机的发展，该领域的研究活动有了极大的发展。大量研究论文、会议论文汇编、书籍章节，甚至教科书都关注这个课题[3,4]。提出了许多技术，它们在计算复杂性、空间分辨率、时间分辨率、噪声、临床治疗方案、灵活性以及伪像各方面具有不同的折中平衡。
1.3.2 Radon(雷登)变换
CT的基本思想源于1917年奥地利数学家Radon提出的Radon变换。
Radon变换的内容可以表述为：若已知某函数
，
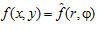如图1.4所示，其沿直线S的线积分为：
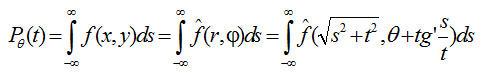(1.1)
则
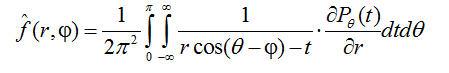(1.2)
式(1.1)为Radon变换，实际上就是物体的投影，式(1.2)为Radon反变换，即根据投影数据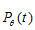
重建函数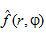
。
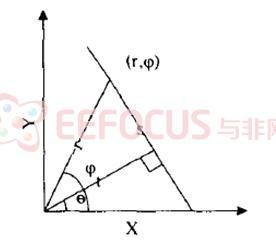
图1.4 Radon变换原理
1.3.3 傅里叶切片定理
傅里叶切片定理的含义是：平行投影的一维傅里叶变换等同于原始物体的二维傅里叶变换的一个切片。即是指出线性衰减系数函数f(x,y)在某一方向上的投影函数gθ(R)的一维傅立叶变换函数Gθ(ρ)是f(x,y)的二维傅立叶变换函数F(u,v)或F(ρ,θ)(极坐标形式)在(ρ,θ)平面上沿同一方向且过原点的直线上的值，如图1.5所示。
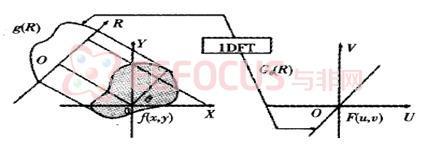
图1.5 中心切片定理示意图
为此，我们在不同的角度下取得足够多的投影函数数据，并作它们的傅立叶变换，那么变换后的数据就将充满整个(u,v)平面。一旦频域函数F(u,v)或F(ρ,θ)的全部值得到后，将其作一次傅立叶反变换，就得到原始的衰减系数函数f(x,y),即
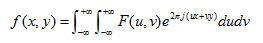(1.3)
令u=ρcosθ，v=ρsinθ，则式(1)可进一步变形为
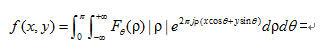
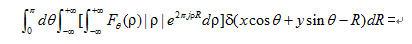
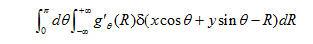(1.4)
式中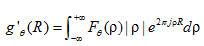
，表示对投影函数
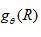的傅里叶变换函数进行滤波变换，其中
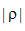为滤波函数。
由傅立叶变换性质可知，频域中的滤波运算可等效地在空域中用卷积运算来完成，因此由(2)可得到
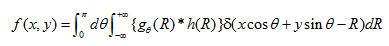（1.5）
式中h(R)为滤波函数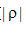
的空域形式，
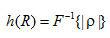，因而这种方法也称为卷积反投影方法。
利用中心切片定理[5]及二维FFT反变换法重建图像，由于勿须反投影运算,因而速度快,但图像重建过程中,需要内插运算，因而重建图像精度相对较低。
首先求出各投影数据的一维傅里叶变换，在不同的投影角度下所到的一维变换函数可构成完整的二维傅里叶变换函数，将此二维函数作一次反傅里叶变换，就得到重建图像。为了在二维逆变换中采用快速傅里叶变换算法，通常在逆变换前要将极坐标转化为直角坐标的形式。
傅里叶变换法重建法的特点是变换速度快，但精度不如滤波反投影法。算法的关键是将弧形的的极坐标数据转换成直角坐标数据时，由于在边缘区高频数据减少，因而造成误差，但傅里叶变换重建法重建速度比滤波反投影可提高2-3倍一在弧形极坐标数据向直角坐标系转化时，最简单的是最邻近内插法，当然这种方法精度最低，双线性内插重建图像精度好于最邻近内插法，而且计算又不复杂。
解决的方法是扩大计算区域，通过外延数据附加上一些格外的点，即计算更多的像素点以减小边缘的误差。如重建图像为M×M，则可计算3M×3M区域内的FFT变换，当然这是以增加了计算量为代价的。傅里叶变换重建图像算法在内插网格点上进行一些适当的选择。如使径向点取在直角坐标网格的线上，这样只需一次内插，而重建图像精度有了较大的改进。
1.3.4 CT图像重建的几种算法
在实际重建当中所存在的问题是，虽然Radon给出了一个数学公式，但是我们需要一个有效的算法来解决它，图像重建的算法有很多，大致分为三类：精确算法、近似算法和迭代算法。近似算法中，以滤波反投影算法(Filter back projection，FBP)最具代表性，应用最为广泛。选代算法中，代数重建算法(Algebraic reconstruction technique，ART)是提出最早并最为人们熟悉的算法。迭代型算法(如代数重建算法等)具有许多优点，但由于计算量大、重建时间长．在很长一段时间内限制了其在医学和工业CT领域的应用。提高迭代型算法的计算速度一直是人们关注的问题。近年来人们提出了不少提高迭代算计算速度的方法，加上近年来计算机计算速度的迅速提高，迭代算法重新受到人们青睐。此外，由于应用的需要，局部重建算法(Local Reconstruction Algorithm， LocalRA)也在近十年中有了较大的发展。在传统全局CT算法中，即使重建物体断面中一个小区域的图像，也得围绕整个断面采集投影数据。而局部重建算法，仅需围绕感兴趣区域及其邻域采集投影数据，即可重建感兴趣区域的图像。局部重建算法可减少数据采集时间和重建时间，降低人体(或生物体)的放射摄入量。
1.3.5国内外研究现状
同类课题所研究的技术基本上被国外所垄断，国内尚未有人提出，国内现在所使用的技术是利用PC机上软件来实现图像的重构，所需时间较长，如果用FPGA来实现的话，速度可以提高数十乃至上百倍。
1.4研究背景及意义
在当今社会大力发展医疗卫生条件的背景下，许多医院迫切需要先进的CT来为患者诊断病情，现在的CT技术被国外所垄断，设备也都在200万以上，只有极少数医院有能力配备，所以急需研发具有自主知识产权的产品，把价格控制在50万以内。CT的关键技术之一是快速断层图像重建技术，本课题的立足点就在于利用FPGA的高度并行性，实现CT断层图像重建算法，满足实际产品速度要求，为实现CT国产化准备，推动社会医疗卫生条件的发展。
