第二章 滤波反投影算法
2.1 滤波反投影算法介绍
尽管傅里叶切片定理提供了断层成像重建的一个直接方案,在真正实现过程中,它提出了一些难题。首先,傅里叶空间中产生的采样模式不是笛卡儿坐标的。傅里叶切片定理说明一次投影的傅里叶变换是二维傅里叶空间中通过原点的一条直线。结果,不同投影采样落到极坐标栅格上。为了执行二维傅里叶变换,这些采样不得不被插值或重新栅格化到一个笛卡儿坐标中。二维频率域中的插值不像真实空间中的插值一样直接。在真实空间里,一个插值误差局限于像素所在的小区域。然而,对于频域插值,这个特性不再有效,因为二维傅里叶空间中每个采样表示某一个空间频域(在水平和垂直方向上)。于是,在傅里叶空间中一个单独采样点上产生的误差会影响整个图像(经过傅里叶反变换后)的外貌。为阐明傅里叶域插值的敏感性,进行下面的简单实验。扫描一个肩部模体,并在512×512矩阵中重建,矩阵用f(x,y)表示,其中x=0,1,…512,y= 0,1,…,512。下一步,执行图像的二维离散傅里叶变换,得到一个函数F(u,v),其中u=0,1,…,511,v=0,1,…,511。注意F(u,v)是一个512×512复数矩阵。在该矩阵中,F(00)代表图像的直流成分。如果简单地进行函数F(u,v)的离散傅里叶反变换,将得到原始图像f(x,y)。注意函数F(u,v)是我们试图采用平行投影进行估计的量值(傅里叶切片定理)。
直接傅里叶域重建的另一缺点是进行目标重建的困难性。目标重建是在CT中常用的技术,用来检查物体中一个小区域的精密细节。如果能以某种方式把重建“聚焦”在感兴趣区,物体的细节就可以更好地显现。采用直接傅里叶重建方法,需要用大量的0填充F(u,v),以进行必要的频率域插值。傅里叶反变换的大小和目标ROI的尺寸成反比。对非常小的ROI,矩阵尺寸庞大以至无法管理。尽管其他技术可以用来克服其中一些困难,这些技术的实现仍不直截了当。因此,必须研究傅里叶切片定理的替代实现方法。滤波反投影算法是目前得到广泛应用的基于变换法的图像重建算法,它具有重建速度快、空间和密度分辨率高等优点,缺点是对投影数据的完备性要求较高[7],从数学上讲,只有获得被检试件所有的Radon变换数据(完全投影数据)后才能精确重建其切片图像。
2.2 滤波反投影算法公式的推导
我们从傅里叶变换和傅里叶反变换是共扼算子这一众所周知的事实开始。图像函数f(x,y)可以通过傅里叶反变换从它的傅里叶变换F(u,v)中恢复,
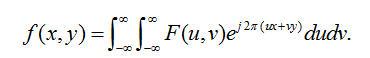 (2.1) (2.1)
与推导傅里叶切片定理时进行的坐标变换类似,我们从笛卡儿直角坐标(u,v)转换到极坐标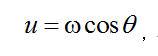 。 。
坐标转换的目的是以更自然的数据采集形式表达数值F(u,v)。坐标转换如下:
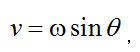 , ,
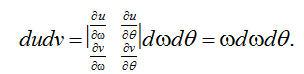 , (2.2) , (2.2)
和
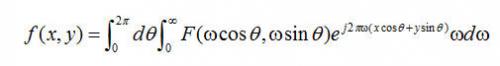 (2.3) (2.3)
将等式(2.2)和(2.3)带入到(3.1),得到
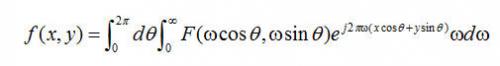 (2.4) (2.4)
利用公式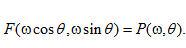 中描述的傅里叶切片定理,我们用 中描述的傅里叶切片定理,我们用 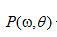 代替 代替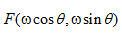 ,建立如下关系: ,建立如下关系:
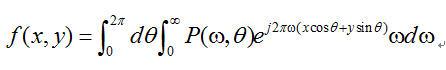
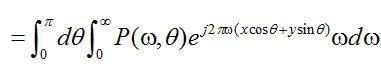 (2.5) (2.5) 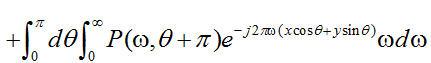 . . 对于平行采样几何束,在投影采样中存在一个微妙的对称性:
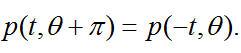 (2.6) (2.6)
通过研究一组相差180°的平行束的采样几何,这个特性可以很容易理解。两组投影正好代表同一组射线路径。基于傅里叶变换的特性,对于相应的傅里叶变换对来说,存在一个简单关系:
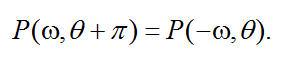 (2.7) (2.7) 将等式(2.7)代入等式(2.5),我们得到下面等式:
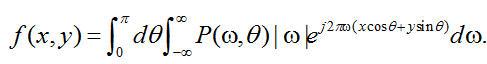 (2.8) (2.8)
通过在旋转坐标系(s,t)中表达上面的等式,并利用等式:
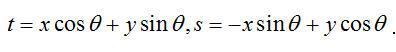 . .
中指出的关系,我们得到下面等式:
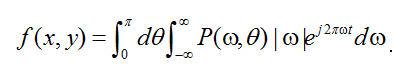 . (2.9) . (2.9) 这里,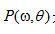 是在角度 是在角度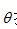 投影的傅里叶变换。内部积分是数值 投影的傅里叶变换。内部积分是数值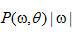 的傅里叶反变换。在空间域,它代表一个经频域响应为 的傅里叶反变换。在空间域,它代表一个经频域响应为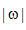 的函数滤波后的投影。我们称之为“滤波投影”。 的函数滤波后的投影。我们称之为“滤波投影”。
如果用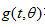 标记等式(2.9)的内部积分所代表的 标记等式(2.9)的内部积分所代表的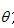 角上的滤波投影: 角上的滤波投影:
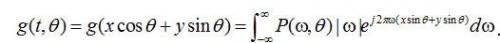 . (2.10) . (2.10)
等式(2.8)可以下面形式重写
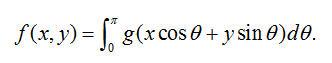 (2.11) (2.11)
变量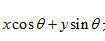 是从点(x,y)到一条通过坐标系原点,并与x轴成 是从点(x,y)到一条通过坐标系原点,并与x轴成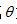 角的直线的距离。等式(2.11)说明,重建图像f(x,y)在位置(x,y),是通过该点的所有滤波投影采样的累加。另外,我们还可以选择关注一个特定滤波投影采样,研究它对重建图像的贡献。因为 角的直线的距离。等式(2.11)说明,重建图像f(x,y)在位置(x,y),是通过该点的所有滤波投影采样的累加。另外,我们还可以选择关注一个特定滤波投影采样,研究它对重建图像的贡献。因为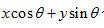 代表与产生投影采样的射线路径重叠的一条直线, 代表与产生投影采样的射线路径重叠的一条直线,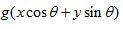 的强度沿着直线均匀地加到重建图像。结果,滤波投影采样的值沿着整个直线路径被“涂抹”或“叠加”。 的强度沿着直线均匀地加到重建图像。结果,滤波投影采样的值沿着整个直线路径被“涂抹”或“叠加”。
|