|
 
- UID
- 1029342
- 性别
- 男
|

在数学上,递推关系(recurrencerelation),也就是差分方程(difference equation),是一种递推地定义一个序列的方程式:序列的每一项目是定义为前一项的函数。
举个例子(户口调查映射(logisticmap)):
 某些简单定义的递推关系式可能拥有非常复杂的(混乱的)行为,且有时候在数学的领域称为非线性分析中被物理学家和数学家所研究。 某些简单定义的递推关系式可能拥有非常复杂的(混乱的)行为,且有时候在数学的领域称为非线性分析中被物理学家和数学家所研究。
解一个递推关系式的意思,就是得到一种n的非递回函数33
[编辑]常系数线性齐次递推关系式线性字眼的意思是序列的每一项目是被定义为前一项的一种线性函数。系数和常数可能视 n 而定,甚至是非线性地。
一种特别的情况是当系数并不依照 n 而定。
齐次意思为关系的常数项为零。
为了要得到线性递回唯一的解,必须有一些起始条件,就是序列的第一个数字无法依照该序列的其他数字而定时,且必须设定为某些数值。
[编辑]解线性递推关系式递推关系式的解通常是由系统的方法中找出来,通常借由使用生成函数(generatingfunction) (形式幂级数(formalpowerseries))或借由观察rn是一种对r的特定数值之解的事实。
二阶递推关系式的形式:
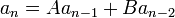 我们拥有解为rn: 我们拥有解为rn:
 两边除以rn − 2我们可以得到: 两边除以rn − 2我们可以得到:
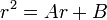 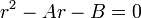 这就是递推关系式的特征方程。解出r可获得两个根(roots)λ1,λ2,且如果两个根是不同的,我们可得到解为 这就是递推关系式的特征方程。解出r可获得两个根(roots)λ1,λ2,且如果两个根是不同的,我们可得到解为
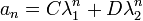 而如果两个根是相同的(当A2+4B=0),我们得到 而如果两个根是相同的(当A2+4B=0),我们得到
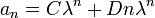 C 和 D 都是常数。 C 和 D 都是常数。
换句话说,将这种an =Aan − 1 +B形式的方程式,用 2 代入 n 后,就得到上述的r2 =Ar + B。常数 "C" 和 "D" 可以从"边界条件(side conditions)" 中得到,通常会像是“已知a0 =c1, a1 =c2”。
[编辑]范例:斐波那契数(Fibonacci Number)斐波那契数是使用一种线性递推关系式来定义:
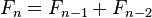 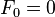  设若: 设若: 当n趋于无限大之极限值存在,则其值为 当n趋于无限大之极限值存在,则其值为 = Φ恰为黄金分割之ㄧ值,1.618....,另一值则为0.618....,两值互为倒数,也就是说1.618....分之1=0.618....,反之亦然。 = Φ恰为黄金分割之ㄧ值,1.618....,另一值则为0.618....,两值互为倒数,也就是说1.618....分之1=0.618....,反之亦然。
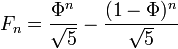 起始条件为: 起始条件为:
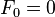  因此,斐波那契数的序列为: 因此,斐波那契数的序列为:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89 ...[编辑]常系数非齐次线性递推关系对于常系数非齐次线性递推关系,我们可以用待定系数法来求出它的一个特解,而它的通解就是这个特解与对应的齐次递推关系的通解的和。也可以使用迭代法求解,但只能得到确切的数值解,不能直接以解析式作答,该方法可利用计算机求解。
[编辑]时域经典法求解一般情况下,常系数线性差分方程可以写作:
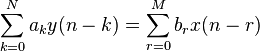 则对应的齐次方程形式为: 则对应的齐次方程形式为:
 则特征方程为: 则特征方程为:
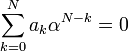 当特征根非重根时,齐次解为: 当特征根非重根时,齐次解为:
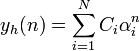 当特征根为重根时,若α1为特征方程的K重根,齐次解为: 当特征根为重根时,若α1为特征方程的K重根,齐次解为:
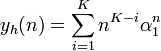 特解yp(n) =D(n)的形式由激励函数x(n)的形式决定。 特解yp(n) =D(n)的形式由激励函数x(n)的形式决定。
一般情况,当激励函数x(n)代入方程。
方程右方出现nk的形式,则特解选择
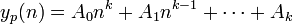 当方程右方出现an的形式,则特解选择 当方程右方出现an的形式,则特解选择
当a不是特征根时
yp(n) =Aan当a是特征根时
yp(n) =(A1n +A0)an当a为r重根时
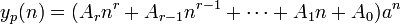 将特解带入原方程,求出待定系数。根据边界条件,可求出齐次节待定系数。 将特解带入原方程,求出待定系数。根据边界条件,可求出齐次节待定系数。
[编辑]例子我们用待定系数法来解以下的常系数非齐次线性递推关系:
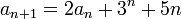 对应的齐次递推关系 对应的齐次递推关系
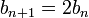 的齐次解是: 的齐次解是:
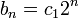 我们猜测特解的形式为: 我们猜测特解的形式为:
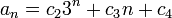 代入原递推关系中,我们便得到: 代入原递推关系中,我们便得到:
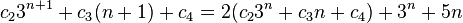 比较等式两端的3n项的系数,可得: 比较等式两端的3n项的系数,可得:
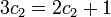 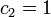 比较等式两端的n项的系数,可得: 比较等式两端的n项的系数,可得:
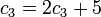 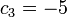 比较等式两端的常数项,可得: 比较等式两端的常数项,可得:
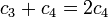  因此原递推关系的通解为: 因此原递推关系的通解为:
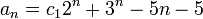 [编辑]与差分方程的关系数值求解常微分方程时,经常会遇到递归关系。例如,求解如下初值问题时 [编辑]与差分方程的关系数值求解常微分方程时,经常会遇到递归关系。例如,求解如下初值问题时
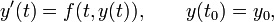 如采用欧拉法和步长h,可以通过如下递归关系计算y0= y(t0), y1 =y(t0 + h),y2 =y(t0 + 2h),... 如采用欧拉法和步长h,可以通过如下递归关系计算y0= y(t0), y1 =y(t0 + h),y2 =y(t0 + 2h),...
yn+ 1 = yn +hf(tn,yn).线性一阶微分方程组可以用离散化条目中介绍的方法解析地精确离散化。 |
|