什么?你问我什么是极大似然估计么?这个嘛,看看你手边的概率或统计教材吧。没有么?那就到维基百科上去看看。
1. 数据与模型我们要使用的数据来自于“MASS”包中的geyser数据。先把数据调出来,看看它长什么样子。
> geyser waiting duration1 80 4.01666672 71 2.15000003 57 4.00000004 80 4.00000005 75 4.0000000......该数据采集自美国黄石公园内的一个名叫Old Faithful 的喷泉。“waiting”就是喷泉两次喷发的间隔时间,“duration”当然就是指每次喷发的持续时间。在这里,我们只用到“waiting”数据,为了简单一点,可以使用attach()函数。
> attach(geyser)
2. 模型绘制出数据的频率分布直方图:
> hist(waiting)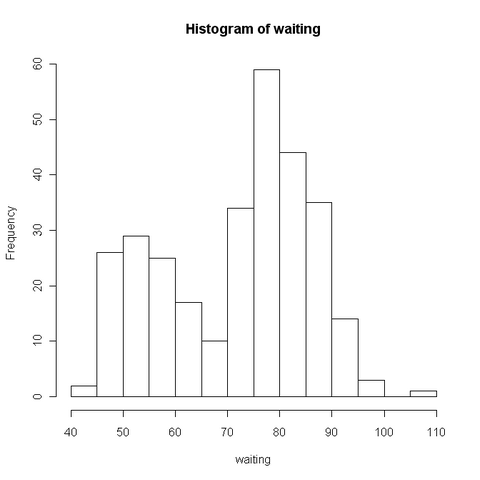
从图中可以看出,其分布是两个正态分布的混合。可以用如下的分布函数来描述该数据
f
(x)=pN
(x
i
;μ
1
,σ
1
)+(1−p)N
(x
i
;μ
2
,σ
2
)
该函数中有5个参数[latex p
、
\mu_1
、
\sigma_1
、
\mu_2
、
\sigma_2$需要确定。上述分布函数的对数极大似然函数为:
l=∑
n
i=1
log
{pN
(x
i
;μ
1
,σ
1
)+(1−p)N
(x
i
;μ
2
,σ
2
)}
3. 估计3.1. 在R中定义对数似然函数:> #定义log-likelihood函数> LL<-function(params,data)+ {#参数"params"是一个向量,依次包含了五个参数:p,mu1,sigma1,+ #mu2,sigma2.+ #参数"data",是观测数据。+ t1<-dnorm(data,params[2],params[3])+ t2<-dnorm(data,params[4],params[5])+ #这里的dnorm()函数是用来生成正态密度函数的。+ f<-params[1]*t1+(1-params[1])*t2+ #混合密度函数+ ll<-sum(log(f))+ #log-likelihood函数+ return(-ll)+ #nlminb()函数是最小化一个函数的值,但我们是要最大化log-+ #likeilhood函数,所以需要在“ll”前加个“-”号。+ }3.2. 参数估计> #用hist函数找出初始值> hist(waiting,freq=F)> lines(density(waiting))> #拟合函数####optim####> geyser.res<-nlminb(c(0.5,50,10,80,10),LL,data=waiting,+ lower=c(0.0001,-Inf,0.0001,-Inf,-Inf,0.0001),+ upper=c(0.9999,Inf,Inf,Inf,Inf))> #初始值为p=0.5,mu1=50,sigma1=10,mu2=80,sigma2=10> #LL是被最小化的函数。> #data是拟合用的数据> #lower和upper分别指定参数的上界和下界。3.3. 估计结果> #查看拟合的参数> geyser.res$par[1] 0.3075937 54.2026518 4.9520026 80.3603085 7.5076330> #拟合的效果> X<-seq(40,120,length=100)> #读出估计的参数> p<-geyser.res$par[1]> mu1<-geyser.res$par[2]> sig1<-geyser.res$par[3]> mu2<-geyser.res$par[4]> sig2<-geyser.res$par[5]> #将估计的参数函数代入原密度函数。> f<-p*dnorm(X,mu1,sig1)+(1-p)*dnorm(X,mu2,sig2)> #作出数据的直方图> hist(waiting,probability=T,col=0,ylab="Density",+ ylim=c(0,0.04),xlab="Eruption waiting times")> #画出拟合的曲线> lines(X,f)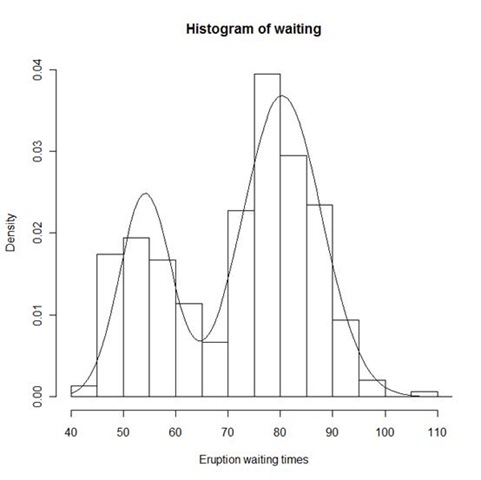
> detach()小结从上面的例子可以看出,在R中作极大似然估计,主要就是定义似然后函数,然后再用nlminb函数对参数进行估计。 |