在做分类时常常需要估算不同样本之间的相似性度量(Similarity Measurement),这时通常采用的方法就是计算样本间的“距离”(Distance)。采用什么样的方法计算距离是很讲究,甚至关系到分类的正确与否。
本文的目的就是对常用的相似性度量作一个总结。
本文目录:
1. 欧氏距离
2. 曼哈顿距离
3. 切比雪夫距离
4. 闵可夫斯基距离
5. 标准化欧氏距离
6. 马氏距离
7. 夹角余弦
8. 汉明距离
9. 杰卡德距离 & 杰卡德相似系数
10. 相关系数 & 相关距离
11. 信息熵
1. 欧氏距离(Euclidean Distance)
欧氏距离是最易于理解的一种距离计算方法,源自欧氏空间中两点间的距离公式。
(1)二维平面上两点a(x1,y1)与b(x2,y2)间的欧氏距离:
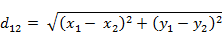
(2)三维空间两点a(x1,y1,z1)与b(x2,y2,z2)间的欧氏距离:
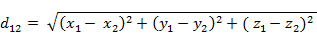
(3)两个n维向量a(x11,x12,…,x1n)与 b(x21,x22,…,x2n)间的欧氏距离:

也可以用表示成向量运算的形式:
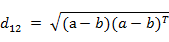
(4)Matlab计算欧氏距离
Matlab计算距离主要使用pdist函数。若X是一个M×N的矩阵,则pdist(X)将X矩阵M行的每一行作为一个N维向量,然后计算这M个向量两两间的距离。
例子:计算向量(0,0)、(1,0)、(0,2)两两间的欧式距离
X = [0 0 ; 1 0 ; 0 2]
D = pdist(X,'euclidean')
结果:
D =1.0000 2.0000 2.2361
2. 曼哈顿距离(Manhattan Distance)
从名字就可以猜出这种距离的计算方法了。想象你在曼哈顿要从一个十字路口开车到另外一个十字路口,驾驶距离是两点间的直线距离吗?显然不是,除非你能穿越大楼。实际驾驶距离就是这个“曼哈顿距离”。而这也是曼哈顿距离名称的来源, 曼哈顿距离也称为城市街区距离(City Block distance)。
(1)二维平面两点a(x1,y1)与b(x2,y2)间的曼哈顿距离
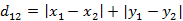
(2)两个n维向量a(x11,x12,…,x1n)与 b(x21,x22,…,x2n)间的曼哈顿距离
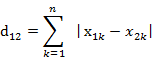
(3) Matlab计算曼哈顿距离
例子:计算向量(0,0)、(1,0)、(0,2)两两间的曼哈顿距离
X = [0 0 ; 1 0 ; 0 2]
D = pdist(X, 'cityblock')
结果:
D = 1 2 3
3. 切比雪夫距离 ( Chebyshev Distance )
国际象棋玩过么?国王走一步能够移动到相邻的8个方格中的任意一个。那么国王从格子(x1,y1)走到格子(x2,y2)最少需要多少步?自己走走试试。你会发现最少步数总是max( | x2-x1 | , | y2-y1 | ) 步 。有一种类似的一种距离度量方法叫切比雪夫距离。
(1)二维平面两点a(x1,y1)与b(x2,y2)间的切比雪夫距离
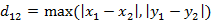
(2)两个n维向量a(x11,x12,…,x1n)与 b(x21,x22,…,x2n)间的切比雪夫距离

这个公式的另一种等价形式是

看不出两个公式是等价的?提示一下:试试用放缩法和夹逼法则来证明。
(3)Matlab计算切比雪夫距离
例子:计算向量(0,0)、(1,0)、(0,2)两两间的切比雪夫距离
X = [0 0 ; 1 0 ; 0 2]
D = pdist(X, 'chebychev')
结果:
D = 1 2 2
4. 闵可夫斯基距离(Minkowski Distance)
闵氏距离不是一种距离,而是一组距离的定义。
(1) 闵氏距离的定义
两个n维变量a(x11,x12,…,x1n)与 b(x21,x22,…,x2n)间的闵可夫斯基距离定义为:

其中p是一个变参数。
当p=1时,就是曼哈顿距离
当p=2时,就是欧氏距离
当p→∞时,就是切比雪夫距离
根据变参数的不同,闵氏距离可以表示一类的距离。
(2)闵氏距离的缺点
闵氏距离,包括曼哈顿距离、欧氏距离和切比雪夫距离都存在明显的缺点。
举个例子:二维样本(身高,体重),其中身高范围是150~190,体重范围是50~60,有三个样本:a(180,50),b(190,50),c(180,60)。那么a与b之间的闵氏距离(无论是曼哈顿距离、欧氏距离或切比雪夫距离)等于a与c之间的闵氏距离,但是身高的10cm真的等价于体重的10kg么?因此用闵氏距离来衡量这些样本间的相似度很有问题。
简单说来,闵氏距离的缺点主要有两个:(1)将各个分量的量纲(scale),也就是“单位”当作相同的看待了。(2)没有考虑各个分量的分布(期望,方差等)可能是不同的。
(3)Matlab计算闵氏距离
例子:计算向量(0,0)、(1,0)、(0,2)两两间的闵氏距离(以变参数为2的欧氏距离为例)
X = [0 0 ; 1 0 ; 0 2]
D = pdist(X,'minkowski',2)
结果:
D = 1.0000 2.0000 2.2361 |