方差(或标准差)反映了随机变量取值的波动程度,但在比较两个随机变量波动性大小时,如果仅看方差(或标准差)有时会产生不合理的现象。产生的原因有:1)随机变量取值有量纲,不同量纲的两个随机变量进行比较没有实际的意义。2)即使量纲相同,取值的大小也有一个相对性的问题,取值较大的随机变量也允许有更大的方差(标准差)。 为此,为比较两个随机变量的波动性大小时,使用如下的变异系数进行比较更合理。
变异系数定义为C_v(X)=sigma(X)/E(X)为X的变异系数。
下面的资料来源于维基百科:
在概率论和统计学中,变异系数,又称“离散系数”,是概率分布离散程度的一个归一化量度,其定义为标准差 与平均值 与平均值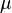 之比。 之比。
变异系数只在平均值不为零时有定义,而且一般适用于平均值大于零的情况。变异系数也被称为标准离差率或单位风险。
变异系数只对由比率标量计算出来的数值有意义。举例来说,对于一个气温的分布,使用开尔文或摄氏度来计算的话并不会改变标准差的值,但是温度的平均值会改变,因此使用不同的温标的话得出的变异系数是不同的。也就是说,使用区间标量得到的变异系数是没有意义的。
变异系数与标准差优点 比起标准差来,变异系数的好处是不需要参照数据的平均值。变异系数是一个无量纲量,因此在比较两组量纲不同或均值不同的数据时,应该用变异系数而不是标准差来作为比较的参考。
[编辑]缺陷- 当平均值接近于0的时候,微小的扰动也会对变异系数产生巨大影响,因此造成精确度不足。
- 变异系数无法发展出类似于均值的置信区间的工具。
应用变异系数在概率论的许多分支中都有应用,比如说在更新理论、排队理论和可靠性理论中。在这些理论中,指数分布通常比正态分布更为常见。
由于指数分布的标准差等于其平均值,所以它的变异系数等于一。变异系数小于一的分布,比如爱尔朗分布称为低差别的,而变异系数大于一的分布,如超指数分布则被称为高差别的。
下面的来自百度百科:
定义变异系数是级差、标准差和方差一样都是反映数据离散程度的绝对值,其数据大小不仅受变量值离散程度的影响,而且还受变量值平均水平大小的影响。一般来说,变量值平均水平高,其离散程度的测度值也大,反之越小。
变异系数是衡量资料中各观测值变异程度的另一个统计量。当进行两个或多个资料变异程度的比较时,如果度量单位与平均数相同,可以直接利用标准差来比较。如果单位和(或)平均数不同时,比较其变异程度就不能采用标准差,而需采用标准差与平均数的比值(相对值)来比较。标准差与平均数的比值称为变异系数,记为C·V。变异系数可以消除单位和(或)平均数不同对两个或多个资料变异程度比较的影响。
已知某良种猪场长白成年母猪平均体重为190kg,标准差为10.5kg,而大约克成年母猪平均体重为196kg,标准差为8.5kg,试问两个品种的成年母猪,那一个体重变异程度大。
此例观测值虽然都是体重,单位相同,但它们的平均数不相同,只能用变异系数来比较其变异程度的大小。
由于,长白成年母猪体重的变异系数:C.V = 10.5 / 190 * 100% = 5.53%
大约克成年母猪体重的变异系数:C.V = 8.5 / 196 * 100% = 4.34%
所以,长白成年母猪体重的变异程度大于大约克成年母猪。
注意,变异系数的大小,同时受平均数和标准差两个统计量的影响,因而在利用变异系数表示资料的变异程度时,最好将平均数和标准差也列出。 |