|
 
- UID
- 1029342
- 性别
- 男
|

2 权系数的设置
一般来说,对辐射源目标特征参数之间重要性没有任何先验信息,采用等加权处理方法,如式(4)所示。它是修正的M距离的一个特例。如果是具有一定先验信息的情况,此时权值可根据先验信息确定。但在实际工,作中,先验信息很难得到,此时可以采用如下的熵值分
析法确定权系数。
2.1 熵的定义[2]
熵在信息论中是一个非常重要的概念,它是不确定性的一种度量。设集合X中各事件出现的概率用n维概率矢量p=(p1,p2,…,pn)表示,且满足 则熵定义为: 则熵定义为:
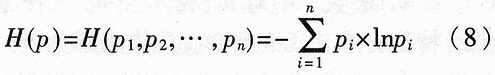
因此,熵H可以看作是n维概率矢量户p=(p1,p2,…,Pn)的函数,称为熵函数。
熵函数H(p)具有以下重要性质:
(1)对称性:概率矢量p=(P1,P2,…,Pn)各分量p1,p2,,…,Pn的次序任意改变时,熵函数H(P)的值不变,即熵值只与集合X总体上的统计特征有关。
(2)非负性:熵函数是一个非负量,即: H(Pl,P2,…,Pn)≥0 (9)
(3)确定性:集合X中只要有一个必然事件,其熵值必为零。
(4)极值性:集合X中各事件以等概率出现时,其熵值为最大,即有:
H(p1,p2,…,pn)≤H(1/n,1/n,…,1/n)=1nn (10)
由熵函数的定义可知,熵值越小,不同类别的分离程度越大。从概率论的角度来看,某一特征的熵值越小则包含的确定性信息越多;反映在分类识别中就是它对识别结果的影响较大,这也意味着设置该特征参数所对应的权值要大一些,以保证识别的精度和准确性。
2.2 熵值分析法设置权重
对于有k类模式的雷达辐射源识别问题,已提取的特片参数共有m个,如式(2)所示。对每一个特征参数Fj;j=1,2,…,m,将其对应的分布区间分为相等的N段,记为rk(j),k=1,2,…,N.注意,这里的分布区间是指k类模式的最大可能的参数分布区间。满足Fj∈rk(j)的样本属于i类的概率为pki(j):
pki(j)=[Nki(j)]/[Nk(j)] (11)
式(11)中,Nk(j)为有Fj∈rk(j)的样本数,Nki(j)为Nk(j)中属于第i类的样本数,于是有:

又设pk(j)为一个样本有Fj∈rk(j)的概率,则有:
pk(j)=[Nk(j)]/N0 (13)
式(12)中N0为总的样本数,即:

从而定义特片Fj的熵值为:

根据熵函数的性质,熵值H(Fi)越小,各类模式在特征Fi上的类间分离性越大,则特征巧对分类的贡献越大,即在识别过程中的权重越大。如果有Fiεrk(j)的所有样本都属于同一类,则有H(Fi)=0。在这种情况下,用这一特征巧就可以实现分类识别。在得到各个特征参数的H(Fi)后,就可以定义相应的归一化权值如下:

需要注意的是,由于识别过程实际上是将侦察所得信号与辐射源数据库中的已知信号相比较,因而可以采用辐射源数据库中的数据作为熵值分析法的样本。这实际上是充分利用已有的知识数据库中的分类信息确定各特征参数在识别中的权值,以期得到较好的识别效果。
获得权系数后,就可根据相似性度量的大小判断一个特征向量应属于哪一类。若已知待识别信号为。,显然满足M'(s,ui)最小的类ωi与样本有着最大的相似度。即:
M'(s,9ui)=min(M'(s,uj))→sεωi (18)
其中i,j=1,2,…,K,K为类的总数,ωi表示第i类。

3 仿真实验及结果分析
在该实验中以雷达知识数据库中11类雷达辐射源的识别问题作为研究对象。所采用的描述雷达类型的特征参数为:载频、重频间隔、脉宽和天线扫描周期。分段数N=100,经计算得到的各个参数在识别中的权重如表1所示。
表1 各参数在识别中的权重
| 特征参数名称 | 载频 | 重频间隔 | 脉宽 | 天线扫描周期 | | 权系数 | 0.37 | 0.24 | 0.2 | 0.19 |
下面考虑对某个已知类型的雷达的一批侦察数据进行处理,计算对该目标的识别率,得到的识别率与信噪比的关系曲线如图1所示。
由图1可以看出,为得到较高的识别率,要求信噪比达到5dB左右。进一步的研究表明该方法对未知的新类型雷达目标具有较好的判断能力;同时,分段数N的大小及由此决定的分段区间对权值的确定有一定的影响。当N足够大时,权系数的变化趋向稳定,最终得到的极限值就可以作为确定权系数的依据。
本方法在实际应用中还要注意特征参数的选取和识别权系数的确定,特别是对先验信息的利用,以期得到更佳的识别效果。 |
|