POLY2——特征交叉的开始但LR的表达能力毕竟是非常初级的。在“辛普森悖论”现象的存在下,只用单一特征进行判断,甚至会得出错误的结论。我们用一个简单的“辛普森悖论”的例子来解释一下为什么特征交叉是重要的。
假设下面是某APP男性用户和女性用户点击广告的数据:
男性用户
点击 曝光 点击率
广告位A 8 530 1.51%
广告位B 51 1520 3.36%
女性用户
点击 曝光 点击率
广告位A 201 2510 8.01%
广告位B 92 1010 9.11%
透过上面两个表格的数据来看,广告位B无论在男性用户还是女性用户中的点击率都高于广告位A,如果我们作为广告需求方构建的CTR模型够精准,理所应当会把广告预算分配给广告位B,而不是广告位A。
那么我们如果去掉性别这个维度,把数据汇总后会得出什么结论呢?
广告位 点击 总曝光 点击率
广告位A 209 3040 6.88%
广告位B 143 2530 5.65%
在汇总结果中,广告位A的点击率居然比广告位B高。我们如果据此进行广告预算的分配,将得出完全相反的结论。可这个结论明显是错误的,广告位A的综合点击率高仅仅是因为其女性用户更多,提高了整体点击率。如果你构建的CTR模型的表达能力不够,很可能被数据“欺骗”。
因此,从“辛普森悖论”中我们能够得出一个结论,低维特征由于对高维特征进行了合并,丢失掉了大量信息。而LR由于只是对单一特征做简单加权,不具备进行特征交叉生成高维特征的能力,所以表达能力是非常初级的。
针对这个问题,当时的算法工程师们经常采用手动组合特征,再通过各种分析手段筛选特征的方法。但这个方法无疑是残忍的,完全不符合“懒惰是程序员的美德”这一金科玉律。更遗憾的是,人类的经验往往有局限性,程序员的时间和精力也无法支撑其找到最优的特征组合。因此采用 PLOY2模型进行特征的“暴力”组合成为了可行的选择。
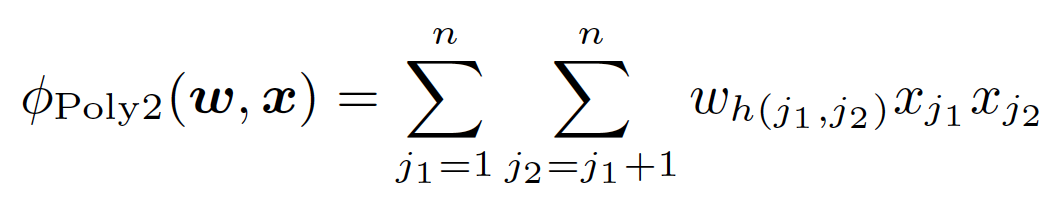
在上面POLY2二阶部分的目标函数中(上式省略一阶部分和sigmoid函数的部分),我们可以看到POLY2对所有特征进行了两两交叉,并对所有的特征组合赋予了权重wh(j1, j2)。POLY2无疑通过暴力组合特征的方式一定程度上解决了特征组合的问题。并且由于本质上仍是线性模型,其训练方法与LR并无区别,便于工程上的兼容。
\"image\"
但POLY2这一模型同时存在着两个巨大的缺陷:
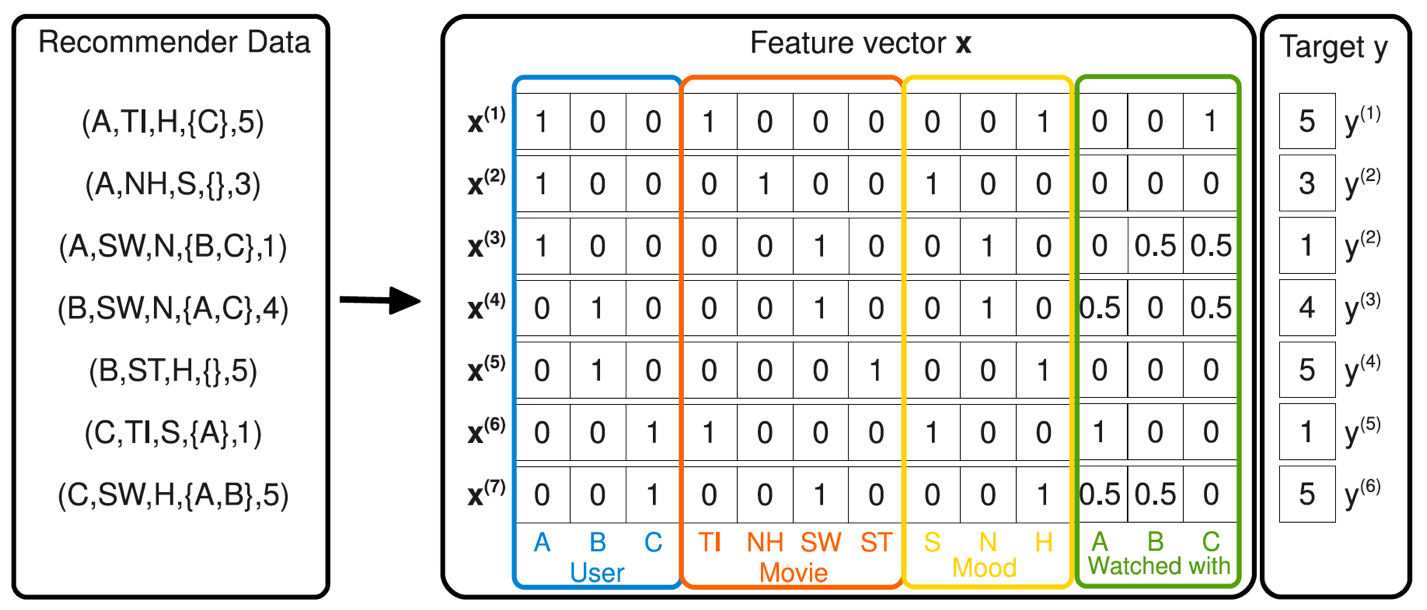
由于在处理互联网数据时,经常采用one-hot的方法处理id类数据,致使特征向量极度稀疏,POLY2进行无选择的特征交叉使原本就非常稀疏的特征向量更加稀疏,使得大部分交叉特征的权重缺乏有效的数据进行训练,无法收敛。
权重参数的数量由n直接上升到n2,极大增加了训练复杂度。 |