红黑树是平衡二叉查找树的一种。为了深入理解红黑树,我们需要从二叉查找树开始讲起。
BST
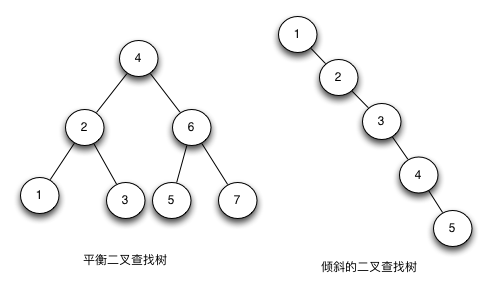
二叉查找树(Binary Search Tree,简称BST)是一棵二叉树,它的左子节点的值比父节点的值要小,右节点的值要比父节点的值大。它的高度决定了它的查找效率。
在理想的情况下,二叉查找树增删查改的时间复杂度为O(logN)(其中N为节点数),最坏的情况下为O(N)。当它的高度为logN+1时,我们就说二叉查找树是平衡的。
BST的查找操作T key = a search keyNode root = point to the root of a BSTwhile(true){ if(root==null){ break; } if(root.value.equals(key)){ return root; } else if(key.compareTo(root.value)<0){ root = root.left; } else{ root = root.right; }}return null;
从程序中可以看出,当BST查找的时候,先与当前节点进行比较:
- 如果相等的话就返回当前节点;
- 如果少于当前节点则继续查找当前节点的左节点;
- 如果大于当前节点则继续查找当前节点的右节点。
直到当前节点指针为空或者查找到对应的节点,程序查找结束。
BST的插入操作Node node = create a new node with specify valueNode root = point the root node of a BSTNode parent = null;//find the parent node to append the new nodewhile(true){ if(root==null)break; parent = root; if(node.value.compareTo(root.value)<=0){ root = root.left; }else{ root = root.right; } }if(parent!=null){ if(node.value.compareTo(parent.value)<=0){//append to left parent.left = node; }else{//append to right parent.right = node; }}
插入操作先通过循环查找到待插入的节点的父节点,和查找父节点的逻辑一样,都是比大小,小的往左,大的往右。找到父节点后,对比父节点,小的就插入到父节点的左节点,大就插入到父节点的右节点上。
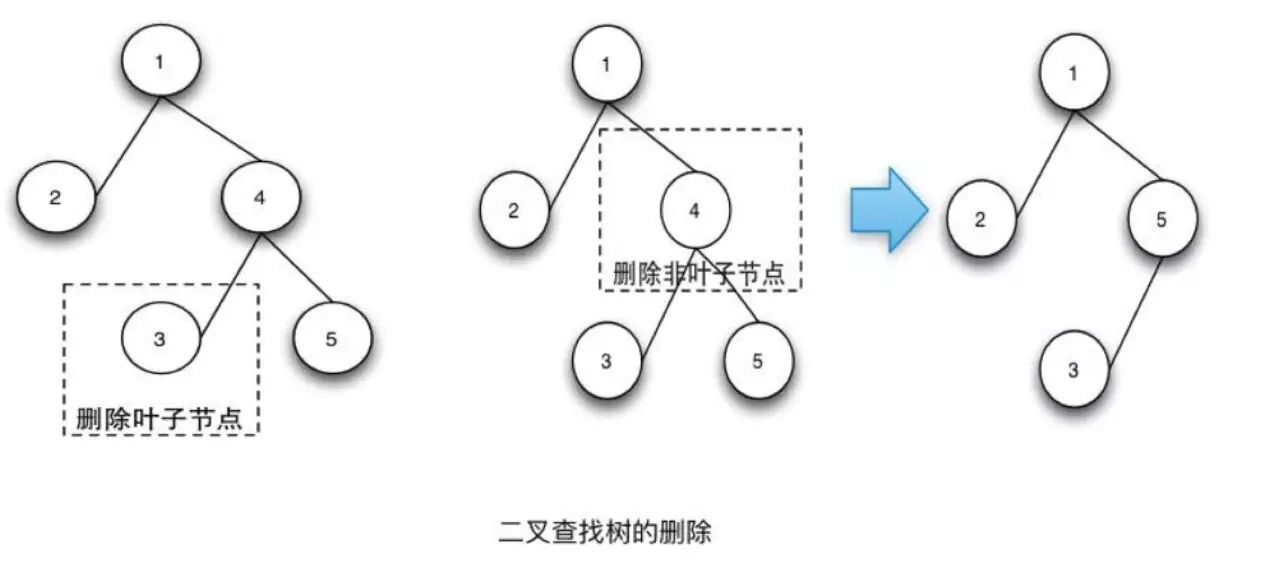
BST的删除操作删除操作的步骤如下:
- 查找到要删除的节点。
- 如果待删除的节点是叶子节点,则直接删除。
- 如果待删除的节点不是叶子节点,则先找到待删除节点的中序遍历的后继节点,用该后继节点的值替换待删除的节点的值,然后删除后继节点。
 |