2.3 匹配函数运算模块
方位压缩的匹配函数为匹配函数再经过FFT变换到频域。在FPGA实现时要把模拟参量量化成离散的数字参量来进行处理。其中γm(RB),RB以雷达到场景中心线的距离Rs为参考进行数字量化,即每一个距离单元的RB=Rs+n deltaR,则RB相对每一个距离单元为常数。慢时间tm以脉冲重复时间1/PRF进行数字量化,相对于每一个方位单元为常数。在设计时,由于γm(RB)对于同一个距离单元来说为常数,所以可以把不同距离单元的γm(RB)按一定顺序存入一个ROM中,在处理不同的距离单元时读取相对应的γm(RB)。αr(tm)实现时用汉明窗。对于exp()采用CORDIC算法生成sin,cos来进行实现。若一个距离单元nan有个采样点,则向量由于PRF为常数,所以仅需设计一个产生向量[-nan/2:nan/2-1]2的模块,即每个时钟周期送出向量[-nan/2:nan/2-1]2中的一个数。匹配函数运算模块的框图,如图2所示。
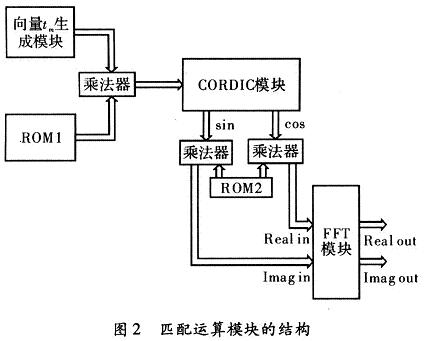
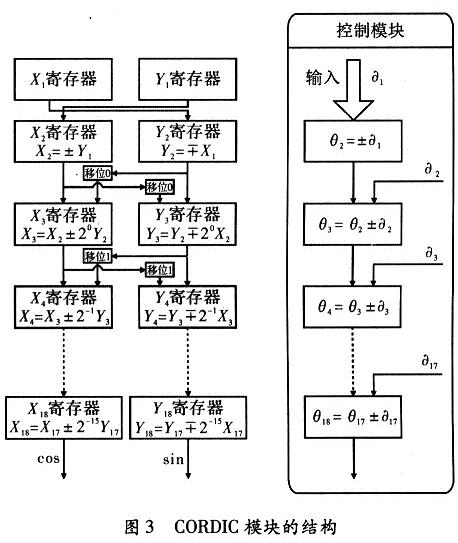
CORDIC模块的实现是匹配函数运算模块设计的重点。CORDIC(Coordinate Rotation Digital Com-puter算法即坐标旋转数字计算方法。主要用于三角函数、双曲线、指数、对数的计算。CORDIC模块采用18级流水线结构来实现,如图3所示。18级寄存器组中下一级寄存器中的输入数据是上一级寄存器的输出数据进行移位后相加或减组合得到的。进行加运算还是减运算完全由控制模块控制。控制模块的输入就是整个CORDIC模块的输入,即要进行sin,cos计算的角度э1。控制模块也采用流水线结构与18级寄存器组一一对应,达到对各级流水线的控制。18级流水线设计需要18个时钟周期来获取第一个计算结果,而只需要一个时钟周期来获取随后的计算结果。流水线结构的特点非常适合应用于方位脉冲压缩匹配函数运算的设计:首先,实时成像需要很高的数据吞吐量,这与流水线结构的优势相符合;其次距离单元的数据是随着时钟依次进入运算模块的,即一个时钟周期读人一个距离单元的数据,这与流水线结构的特点十分的吻合。采用流水线结构实现CORDIC算法,可以使匹配函数的数据在每个周期逐个输出,仅做好同步工作,使匹配函数的数据与距离脉冲压缩结果对应匹配相乘即可。
2.4 匹配相乘模块
匹配相乘模块主要完成的工作,是把距离脉冲压缩的数据经FFT后的结果与匹配函数对应相乘,再把相乘的结果送出。匹配相乘模块的核心是复数乘法器。复数乘法器是由4个普通乘法器和两个加法器组成。假设完成(a+bi)×(c+di)的操作,先分别计算a×c,a×d,b×c,b×d这4个实数与实数的乘法运算,再把减法运算a×c-b×d结果作为复数乘法器输出的实部,加法运算a×d+b×c的结果作为复数乘法器输出的虚部。
对数据的同步也是设计的重点。因为距离脉冲压缩经FFT后的数据与匹配函数的数据并不是同时进入匹配相乘模块。距离脉冲压缩经FFT后的数据较先进入,主要是因为匹配函数运算的CORDIC采用流水线结构,需要18个时钟周期来获取第一个计算结果而产生匹配函数数据的延迟。所以应该对匹配相乘模块对距离脉冲压缩经FFT后的数据进行缓冲。缓冲采用FIFO模块来实现。FIFO可以采用自带的IP core。
3 波形仿真与性能分析
验证方法采用比对的方法,即单个目标点的仿真数据分别进行理论方位脉冲压缩仿真和基于FPGA的方位脉冲压缩仿真,并将得到的仿真结果进行比对。仿真数据中一个距离单元的点数为16 384点。验证过程是首先在。Matlab软件环境下对单个点目标的一个距离单元进行方位脉冲压缩的仿真,即理论仿真,然后再在Modelsim环境下对该距离单元进行方位脉冲压缩的FPGA仿真,并将得到的结果与Matlab下得到的理论结果进行比较。其比较的波形,如图4所示。
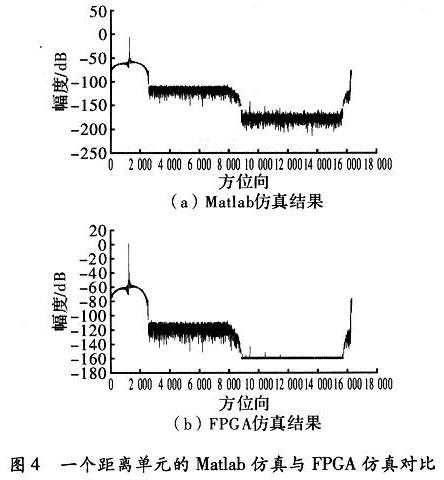
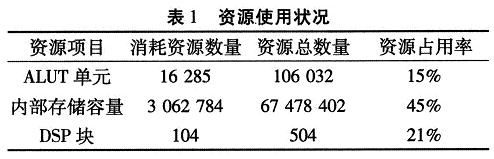
选用Ahera公司芯片EP2S130F780C5进行测试。稳定工作时时钟频率可以达到150 MHz。
4 结束语
方位脉冲压缩系统是这个R-D算法在FPGA实现的关键。文中给出的方案通过实验验证能够达到设计的要求。实验表明,随着可编程器件规模、速度的不断提高,采用FPGA实现高速数字信号处理的算法具有可行性和优越性。 (编辑:chiying) |