|
 
- UID
- 871057
- 性别
- 男
|

摘要 对超宽带通信室内修正S—V信道模型的进行仿真,在分析S—V信道模型的参数特点的基础上,探讨修正S—V信道模型的数学模型的建立方法,在CM4的非视距(NLOS)信道环境下,用Matlab进行仿真实验,结果表明修正S—V信道模型更接近实际,比S—V信道模型具有更好的信道冲激响应特性,能够更好地应用于超宽带通信系统性能的信道传榆特性研究。
关键词 超宽带;修正信道;Matiab仿真
超宽带(Ultrawideband,UWB)无线通信是一种能够和其他通信系统共享频谱资源的新型无载波通信技术。由于UWB信号的功率谱密度远低于其他通信系统噪声的容许门限,所以基本感觉不到UWB信号的存在,同时为恢复被严重干扰的UWB信号,超宽带通信系统采用信号多次重传的方式提高接收端的信噪比,以保证能够实现信号的有效解调。又考虑到多址接入和保密性的需要,UWB系统为每个用户分配一个惟一的伪随机码,利用这些伪随机码来调制不同用户之间的数据信息,实现多用户通信和提高通信系统的保密性。
目前为止,人们对于超宽带信号的传播问题进行了大量测量,尤其是集中在室内环境信道下的测试较多,由于进行分析的数据量不足,对不同的测量不能进行统一的规范化,已有的超宽带室内统计模型中较为著名的是S—V信道模型,这是一种描述多径按簇分布的信道模型,文中进行仿真研究了修正S—V信道模型,保留原有S—V信道模型中多径成簇到达和能量服从双指数分布的特点,但修正S—V信道模型中每一径的幅度不再服从瑞利分布,而是根据实测结果更加符合对数正态分布,成为研究超宽带系统性能的更好的信道平台。
1 信道测量技术
由于UWB信号的射频带宽通常达到GHz量级,信号传播特性与传统的窄带或宽带连续波信号有着明显的不同,特别在非视距环境下对超宽带信道的测量、分析以及建模将不同于传统的方法,如何获得信道冲激响应是研究信道传播特性的核心问题,因此信道测量是研究信道传输特性的基础。
超宽带通信信道测量技术是利用适当的UWB信号来探索信道,主要有两种测量方法,一是时域测量技术;二是频域测量技术,该技术是利用矢量网络分析仪,在指定频带上选择若干等间隔的离散频率点发射单频信号,得到信道的时域冲激响应及统计量,UWB信道可以用一个时变的脉冲响应表示为
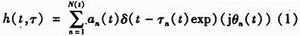
其中,第n径的参数an,τn,θn分别是幅度、时延、相位;N表示多径数目。UWB信道也可以描述为频域自回归模型,表示为
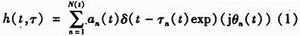
其中,bi是模型参数;p是模型阶数;V(fn)是复白噪声;H(fn,x)是位置x处复频率响应的第n个抽样。2 信道数学模型的建立
2.1 S-V信道模型
由于超宽带技术主要应用于室内环境,所以人们对超宽带信道的建模主要集中在室内环境。由于墙壁、家具、人等障碍物的存在,UWB脉冲通常会发生反射、衍射等现象,且发送端与接收端很少存在视距传播路径(LOS),因此UWB室内传播时的多径现象严重且第一径通常不具有最大能量。到目前为止,人们已经提出了多种UWB室内信道模型,如△-K模型、POCA-NAZA模型、S—V模型和IEEE802.15.3a室内标准信道模型等。目前普遍认可的对于室内超宽带传输特性描述较好的是基于分簇方式的模型,该模型首先由Turin于1972年提出,后来Saleh和Valen zuela在对宽带信号的研究中提出了进一步规范化的模型,得到了普遍认可,即S—V模型,基物理描述如下:多径信号不是按着固定的速率均匀到达接收机,而是以簇(Cluster)的形式,分成一簇一簇地到达。S—V信道模型是一个统计模型,由实测数据建模而成,在该模型中,来自同一个脉冲的多径分量以簇的形式到达接收机,簇到达时间被建模成一个速率为A的泊松过程
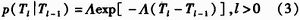
其中,Tl与Tl-1分别表示第l簇和第l-1簇的到达时间。在不考虑空间传播延迟的情况下,可以假设第一簇的到达时间等于零。每一簇内包含多个多径分量,而且多径分量的到达时间也被建模成一个到达速率为λ的泊松过程
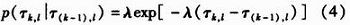
其中,τk,l与τ(k-1),l分别表示第l簇内的第k与第k-1条径的到达时间。用βk,lexp(jθk,l)表示第l簇内的第k径的复数衰减系数,则S—V信道模型的冲击响应可表示为
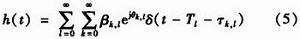
其中,Tl,l=0,1,2,…为第l个到达簇的到达时间,τk,l,k=0,1,2,…为第l个簇中到第k个到达射线的到达时间,T0=0为第一个到达簇的到达时间,τ0l=0为第l个簇中第一条射线到达时间,δ(·)为狄拉克冲激函数,θk,l为在[0,2π)均匀分布的随机变量,|βk,l|为相互独立且服从瑞利分布的随机变量,其平均功率服从双指数分布
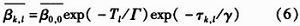
算中, 为第l簇内的第k径的平均功率;Γ为簇功率衰减因子;γ为多径的功率衰减因子。虽然在该统计模型中多径数目可以为无穷大,但是在实际测试中,当l或k比较大时,βk,l近似为零。 为第l簇内的第k径的平均功率;Γ为簇功率衰减因子;γ为多径的功率衰减因子。虽然在该统计模型中多径数目可以为无穷大,但是在实际测试中,当l或k比较大时,βk,l近似为零。
2. 2 修正S-V信道模型
S—V模型是一个适合仿真研究使用的完整的多径模型,但存在几个问题,首先,S—V信道能够准确地反应室内LOS环境的传播规律,但对于NLOS环境的性能明显不足;其次,模型无法准确预测特定环境的多径传播特性;最后,在实际应用中存在模型输入参数获取困难的问题。为与超宽带实测实验中得到的数据更吻合,802.15.3a工作组对S—V模型进行了一些修改,建议利用对数正态分布而不是瑞利分布来描述多径增益幅度,第一簇内部各路径之间是独立的衰减机制,用另一个对数正态分布随机变量表示总多径增益的波动,簇和簇内路径的到达时间分别是用独立的泊松过程来描述,信道冲激响应的相位分别是0或π,因此不存在虚部分量,信道误差系数采用实变量来代替原来的复变量。考虑到UWB信号脉冲经过电介质表面反射出现脉冲翻转的概率是随机的,假设θk,l等概率出现于±π,则修正后的信道模型冲激响应可以表示为
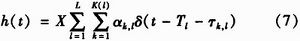
其中,X表示阴影效应对应的对数正态衰落随机变量,它反映了信号总能量的衰落,其分布为20lg10(Xi)~N(0,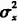 ),L是观测到的簇的数目;K(l)是第l簇内接收到的多径数目,αk,l是第l簇内第k条径的幅度增益,可以表示为αk,l=Pk,lξlβk,l,此处Pk,l等概率地取±1,表赤由反射引起的信号反转,ξl反应第l簇的衰减,βk,l对应第l簇内第k条径的衰减,ξlβk,l也服从正态分布,即20lg10(ξkβk,l)~N(μk,l, ),L是观测到的簇的数目;K(l)是第l簇内接收到的多径数目,αk,l是第l簇内第k条径的幅度增益,可以表示为αk,l=Pk,lξlβk,l,此处Pk,l等概率地取±1,表赤由反射引起的信号反转,ξl反应第l簇的衰减,βk,l对应第l簇内第k条径的衰减,ξlβk,l也服从正态分布,即20lg10(ξkβk,l)~N(μk,l,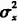 ),此处的 ),此处的 表示簇衰减系数的标准差, 表示簇衰减系数的标准差,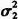 表示径衰减系数的标准差,μk,l表示径衰减系数的均值,可表示为 表示径衰减系数的标准差,μk,l表示径衰减系数的均值,可表示为
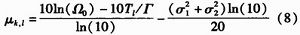
其中,Ω0是第一簇第一径的平均能量。
3 信道仿真及结果分析
基于发射机和接收机的平均距离和是否存在视距分量,推荐4种不同的实测信道,CM1:视距(0~4 m),CM2:非视距(0~4 m),CM3:非视距(4~10 m),CM4:非视距(4~10 m),代表了极端的NLOS多径信道环境。不同环境下的信道模型对应的参考值,如表1所示。

|
|