
第1章介绍
1. 为什么要进行视频压缩?

2. 为什么可以压缩
- 去除冗余信息
- 空间冗余:图像相邻像素之间有较强的相关性
- 时间冗余:视频序列的相邻图像之间内容相似
- 编码冗余:不同像素值出现的概率不同
- 视觉冗余:人的视觉系统对某些细节不敏感
- 知识冗余:规律性的结构可由先验知识和背景知识得到
3. 数据压缩分类
- 无损压缩(Lossless)
- 压缩前解压缩后图像完全一致X=X'
- 压缩比低(2:1~3:1)
- 例如:Winzip,JPEG-LS
- 有损压缩(Lossy)
- 压缩前解压缩后图像不一致X≠X'
- 压缩比高(10:1~20:1)
- 利用人的视觉系统的特性
- 例如:MPEG-2,H.264/AVC,AVS

4. 编解码器
- 编码器(Encoder)
- 解码器(Decoder)
- 编解码器(Codec)
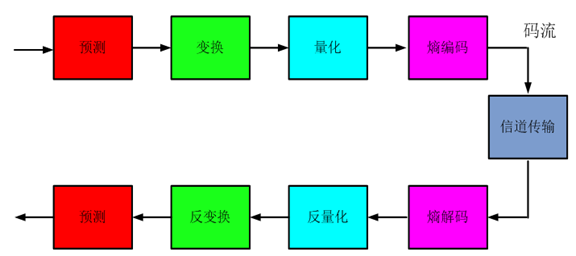
5. 压缩系统的组成
(1) 编码器中的关键技术

(2) 编解码中的关键技术
6. 编解码器实现
- 编解码器的实现平台:
- 超大规模集成电路VLSI
- 数字信号处理器DSP
- 软件
- 编解码器产品:
7. 视频编码标准
编码标准作用:
- 兼容:
- 不同厂家生产的编码器压缩的码流能够被不同厂家的解码器解码
- 高效:
主流的视频编码标准:
- MPEG-2
- MPEG-4 Simple Profile
- H.264/AVC
- AVS
- VC-1
标准化组织:
- ITU:International Telecommunications Union
- VECG:Video Coding Experts Group
- ISO:International Standards Organization
- MPEG:Motion Picture Experts Group
8. 视频传输
- 视频传输:通过传输系统将压缩的视频码流从编码端传输到解码端
- 传输系统:互联网,地面无线广播,卫星
9. 视频传输面临的问题
10. 视频传输差错控制
- 差错控制(Error Control)解决视频传输过程中由于数据丢失或延迟导致的问题
- 差错控制技术:
11. 视频传输的QoS参数
- 数据包的端到端的延迟
- 带宽:比特/秒
- 数据包的流失率
- 数据包的延迟时间的波动
第2章 数字视频
1.图像与视频
- 图像:是人对视觉感知的物质再现。
- 三维自然场景的对象包括:深度,纹理和亮度信息
- 二维图像:纹理和亮度信息

- 视频:连续的图像。
- 视频由多幅图像构成,包含对象的运动信息,又称为运动图像。

2. 数字视频
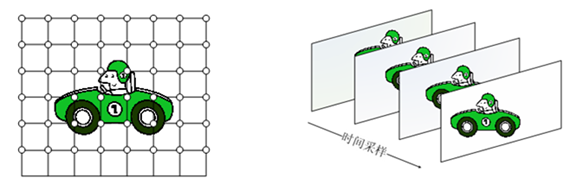
3. 空间采样

4. 数字视频系统

5. 人类视觉系统HVS
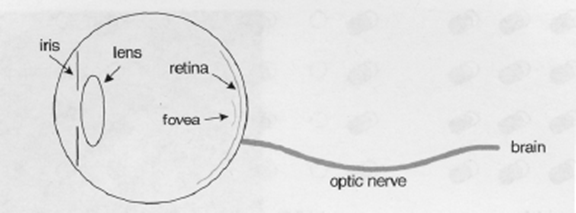
- HVS特点:
- 对高频信息不敏感
- 对高对比度更敏感
- 对亮度信息比色度信息更敏感
- 对运动的信息更敏感
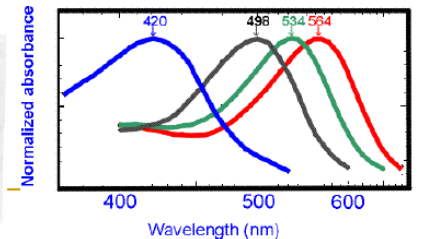
6. 数字视频系统的设计应该考虑HVS的特点:
- 丢弃高频信息,只编码低频信息
- 提高边缘信息的主观质量
- 降低色度的解析度
- 对感兴趣区域(Region of Interesting,ROI)进行特殊处理

7. RGB色彩空间
- 三原色:红(R),绿(G),蓝(B)。
- 任何颜色都可以通过按一定比例混合三原色产生。
- RGB色度空间
- 由RGB三原色组成
- 广泛用于BMP,TIFF,PPM等
- 每个色度成分通常用8bit表示[0,255]

8. YUV色彩空间
- YUV色彩空间:
- Y:亮度分量
- UV:两个色度分量
- YUV更好的反映HVS特点
9. RGB转化到YUV空间
亮度分量Y与三原色有如下关系: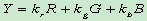
经过大量实验后ITU-R给出了, , ,  , ,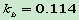

主流的编解码标准的压缩对象都是YUV图像
10. YUV图像分量采样
- YUV图像可以根据HVS的特点,对色度分量下采样,可以降低视频数据量。
- 根据亮度和色度分量的采样比率,YUV图像通常有以下几种格式:

11. 通用 的YUV图像格式
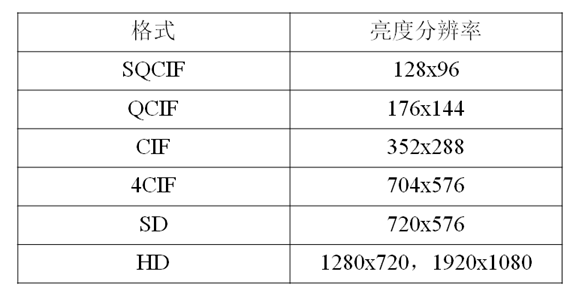
12. 帧和场图像


13. 逐行与隔行图像
- 逐行图像:一帧图像的两场在同一时间得到,ttop=tbot。
- 隔行图像:一帧图像的两场在不同时间得到, ttop≠tbot。

14. 视频质量评价
- 有损视频压缩使编解码图像不同,需要一种手段来评价解码图像的质量。
- 质量评价:
- 客观质量评价
- 主观质量评价
- 基于视觉的视频质量客观评价
- 客观质量评价:通过数学方法测量图像质量评价的方式。
- 优点:
- 缺点:
15. 客观评价的方法
常用的客观评价方法:

16. 主观评价方法
- 主观质量评价:用人的主观感知直接测量的方式。
- 优点:
- 缺点:
- 不容易量化
- 受不确定因素影响,测量结果一般不可重复
- 测量代价高
常用主观评价方法


17. 基于视觉的视频质量客观评价方法
- 基于视觉的视频质量客观评价:将人的视觉特性用数学方法描述并用于视频质量评价的方式。
- 结合了主观质量评价和客观质量评价两方面优点。
- 常用方法:结构相似度(Structural SIMilarity,SSIM)方法。
- 将HVS的特征用数学模型表达出来。
- 未来重要的研究方向
第3章 信息论基础
1. 通信系统的组成
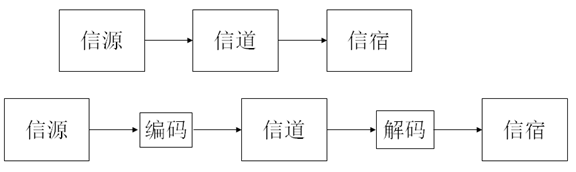
2. 基本概念
- 通信中对信息的表达分为三个层次:信号,消息,信息。
- 信号:是信息的物理层表达,可测量,可描述,可显示。如电信号,光信号。
- 消息:是信息的载体,以文字,语言,图像等人类可以认知的形式表示。
- 信息:不确定的内容。
3. 信息熵
信息的特点

信息的测量
自信息量

条件信息量

4. 信息熵


5. 条件熵和联合熵

6. 熵的性质
- 非负性:信源熵是非负值,即 H(X) >=0;
- 扩展性:信源熵X有M个符号,如果其中一个符号出现的概率趋于零,信源熵就等于剩余M-1个符号的信源熵;
- 极值性(最大信息熵):对于具有M个符号的信源,只有在所有符号等概率出现的情况下,信源熵达到最大值,即
 - 可加性:
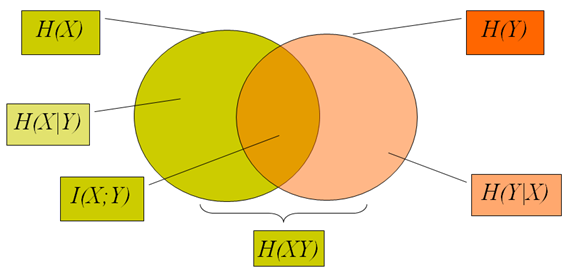
 - 熵不增:条件熵不大于信息熵 H(X|Y) <= H(X);
- 联合熵不大于各信息熵的和,即H(XY) <= H(X) + H(Y)。
7. 互信息量

8. 互信息

- 物理意义:H(X)是X所含的信息,H(X|Y)是已知Y的条件下X还能带来的信息量。那么两者之差就是由于知道Y使得X减少的信息量,也即由Y可以得到的关于X的信息量。
9. 各种熵的关系
11. 信源编码
- 信源编码:将消息符号转变成信道可传输的信息。
- 两个基本问题:
- 用尽可能少的信道传输符号来传递信源消息,提高传输效率;
- 减少由于信道传输符号的减少导致的失真。
12. 离散信源统计特性


13. 离散信源类型:简单无记忆信源和马尔可夫信源

14. 编码分类
- 等长码:在一组码字集合C中的所有码字cm (m = 1,2, …,M),其码长都相同,则称这组码C为等长码。
- 变长码:若码字集合C中的所有码字cm (m = 1,2, …,M),其码长不都相同,称码C为变长码。
15. 平均码长

16. 等长码与变长码比较
- 等长编码将信源输出符号序列的任意一种取值(概率可能不同)都编码成相同长度的输出码字,没有利用信源的统计特性;
- 变长编码可以根据信源输出符号序列各种取值的概率大小不同,将他们编码成不同长度的输出码字,利用了信源的统计特性。因此又称其为熵编码。
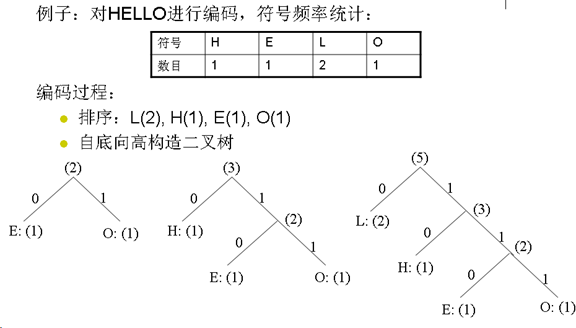
17. Huffman编码
- Huffman编码:典型的变长编码。
- 步骤:
- 将信源符号按概率从大到小的顺序排列,假定p(x1)≥ p(x2)… ≥ p(xn)
- 给两个概率最小的信源符号p(xn-1), p(xn)各分配一个码位"0"和"1",将这两个信源符号合并成一个新符号,并用这两个最小的概率之和作为新符号的概率,结果得到一个只包含(n-1)个信源符号的新信源。称为信源的第一次缩减信源,用S1表表示。
- 将缩减信源S1的符号仍按概率从大到小的顺序排列,重复步骤2,得到只含(n-2)个符号的缩减信源S2。
- 重复上述步骤,直至缩减信源只剩下两个符号为止,此时所剩两个符号的概率之和必为1。然后从最后一级缩减信源开始,依编码路径向前返回,就得到各信源符号所对应的码字。
18. 信道编码
- 信道编码主要考虑如何增加信号的抗干扰能力,提高传输的可靠性,并且提高传输效率。
- 一般是采用冗余编码法,赋予信码自身一定的纠错和检错能力,使信道传输的差错概率降到允许的范围之内。
19. 信道类型
- 根据信道连续与否分类
- 根据信道是否有干扰分类
- 根据信道的统计特性分类
- 无记忆信道
- 有记忆信道
- 恒参信道
- 变参信道
- 对称信道
- 非对称信道
20. 信道容量
- 在信息论中,称信道无差错传输的最大信息速率为信道容量。
- 仙农信道容量公式:
- 假设连续信道的加性高斯白噪声功率为N,信道带宽为B,信号功率为S,则该信道的容量为
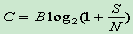 - 由于噪声功率N与信道带宽B有关,则噪声功率N=n0B 。因此,仙农公式还可以表示为
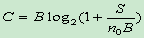
21. 香农信道容量公式的意义
- 在给定B和S/N的情况下,信道的极限传输能力为C,而且此时能够做到无差错传输。如果信道的实际传输速率大于C 值,则无差错传输在理论上就已不可能。因此,实际传输速率一般不能大于信道容量C ,除非允许存在一定的差错率。
- 提高信噪比S/N(通过减小n0或增大S),可提高信道容量C。特别是,若n0->0,则C->∞ ,这意味着无干扰信道容量为无穷大;
- 增加信道带宽B,也可增加信道容量C,但做不到无限制地增加。这是因为,如果 S、n0一定,有
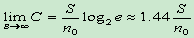 - 维持同样大小的信道容量,可以通过调整信道的B及S/N来达到,即信道容量可以通过系统带宽与信噪比的互换而保持不变。
22. 失真
- 失真:信源的消息经过编解码后不能完全复原
- 在实际的信源和信道编码中,消息的传输并不总是无失真的。
23. 率失真理论
- 仙农定义了信息率失真函数R(D)
- 率失真定理:在允许一定失真度D的情况下,信源输出的信息率可压缩到R(D)。
24. 失真函数
- 失真函数:信源符号X={x1, x2, …..xn},经信道传输接收端符号Y={y1, y2….yn},对于每一对(xi, yj)指定一个非负函数 d(xi, yj),称d(xi, yj)为单个符号的失真度或失真函数。对于连续信源连续信道的情况,常用d(x, y)表示。
- 常用失真函数:
 
- 平均失真度:

文章来源:追随技术WithPassion
|

