概念
最小二乘法多项式曲线拟合,根据给定的m个点,并不要求这条曲线精确地经过这些点,而是曲线y=f(x)的近似曲线y= φ(x)。
原理[原理部分由个人根据互联网上的资料进行总结,希望对大家能有用]
给定数据点pi(xi,yi),其中i=1,2,…,m。求近似曲线y= φ(x)。并且使得近似曲线与y=f(x)的偏差最小。近似曲线在点pi处的偏差δi= φ(xi)-y,i=1,2,...,m。
常见的曲线拟合方法:
1.使偏差绝对值之和最小
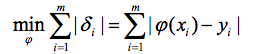
2.使偏差绝对值最大的最小
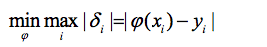
3.使偏差平方和最小
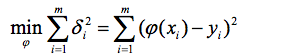
按偏差平方和最小的原则选取拟合曲线,并且采取二项式方程为拟合曲线的方法,称为最小二乘法。
推导过程:
1. 设拟合多项式为:

2. 各点到这条曲线的距离之和,即偏差平方和如下:
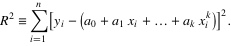
3. 为了求得符合条件的a值,对等式右边求ai偏导数,因而我们得到了:

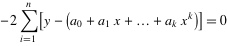
.......
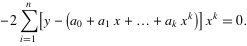
4. 将等式左边进行一下化简,然后应该可以得到下面的等式:
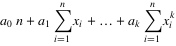
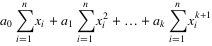
.......
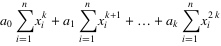
5. 把这些等式表示成矩阵的形式,就可以得到下面的矩阵:
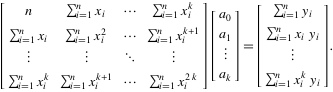
6. 将这个范德蒙得矩阵化简后可得到:

7. 也就是说X*A=Y,那么A = (X'*X)-1*X'*Y,便得到了系数矩阵A,同时,我们也就得到了拟合曲线。 |