|
 
- UID
- 1029342
- 性别
- 男
|

描述在基本的网络搭建完成后,学校为了方便管理还需要对所有的服务器进行编组,网络所的老师找到了小Hi和小Ho,希望他俩帮忙。
老师告诉小Hi和小Ho:根据现在网络的情况,我们要将服务器进行分组,对于同一个组的服务器,应当满足:当组内任意一个连接断开之后,不会影响组内服务器的连通性。在满足以上条件下,每个组内的服务器数量越多越好。
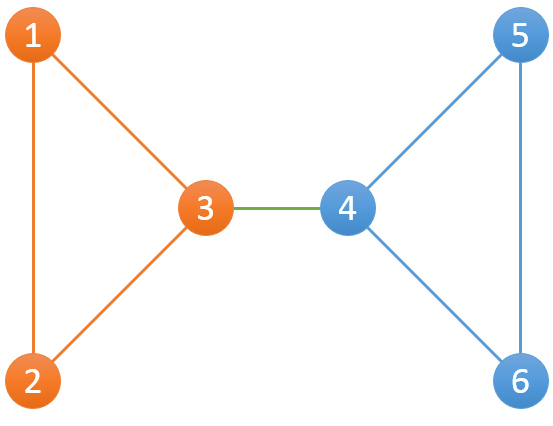
比如下面这个例子,一共有6个服务器和7条连接:

其中包含2个组,分别为{1,2,3},{4,5,6}。对{1,2,3}而言,当1-2断开后,仍然有1-3-2可以连接1和2;当2-3断开后,仍然有2-1-3可以连接2和3;当1-3断开后,仍然有1-2-3可以连接1和3。{4,5,6}这组也是一样。
老师把整个网络的情况告诉了小Hi和小Ho,小Hi和小Ho要计算出每一台服务器的分组信息。
提示:边的双连通分量
输入第1行:2个正整数,N,M。表示点的数量N,边的数量M。1≤N≤20,000, 1≤M≤100,000
第2..M+1行:2个正整数,u,v。表示存在一条边(u,v),连接了u,v两台服务器。1≤u<v≤N
保证输入所有点之间至少有一条连通路径。
输出第1行:1个整数,表示该网络的服务器组数。
第2行:N个整数,第i个数表示第i个服务器所属组内,编号最小的服务器的编号。比如分为{1,2,3},{4,5,6},则输出{1,1,1,4,4,4};若分为{1,4,5},{2,3,6}则输出{1,2,2,1,1,2}
样例输入6 71 21 32 33 44 54 65 6样例输出21 1 1 4 4 4提示:对于一个无向图,当我们把图中所有的桥都去掉以后,剩下的每一个区域就是我们要求的边的双连通分量。比如:
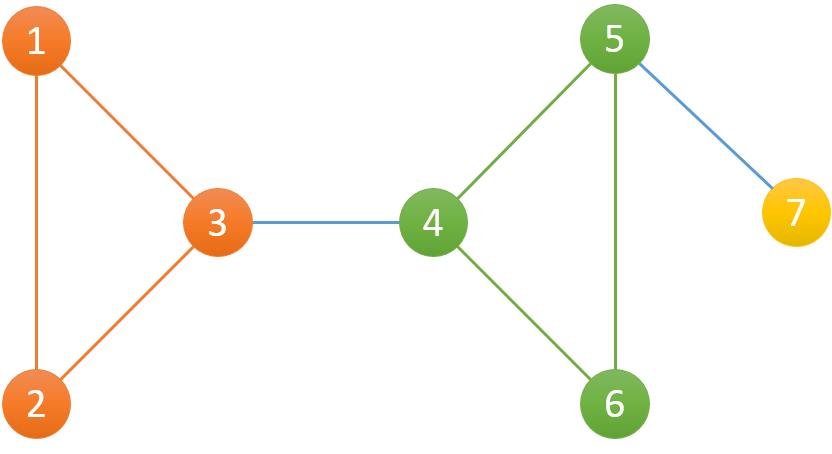
其中{1,2,3},{4,5,6},{7}各为一个组。
直观的做法自然先用上周的算法求出所有桥,去掉所有桥之后再做DFS求出每一个连通子图。我们这周要介绍一种更"抽象"的算法,通过在Tarjan算法当中巧妙地用一个栈来统计出每一个组内的节点,其代码如下:
[cpp] view plain copy
- void dfs(int u) {
- //记录dfs遍历次序
- static
int counter = 0;
- //记录节点u的子树数
- int children = 0;
- ArcNode *p = graph.firstArc;
- visit = 1;
- //初始化dfn与low
- dfn = low = ++counter;
- //将u加入栈
- stack[++top] = u;
- for(; p != NULL; p = p->next) {
- int v = p->adjvex;
- //节点v未被访问,则(u,v)为树边
- if(!visit[v]) {
- children++;
- parent[v] = u;
- dfs(v);
- low = min(low, low[v]);
- if (low[v] > dfn) {
- printf("bridge: %d %d\n", u, v); // 该边是桥
- bridgeCnt++;
- }
- }
- //节点v已访问,则(u,v)为回边
- else
if(v != parent) { - low = min(low, dfn[v]);
- }
- }
- if (low == dfn)
- {
- // 因为low == dfn,对(parent,u)来说有dfn > dfn[ parent ],因此low > dfn[ parent ]
- // 所以(parent,u)一定是一个桥,那么此时栈内在u之前入栈的点和u被该桥分割开
- // 则u和之后入栈的节点属于同一个组
- 将从u到栈顶所有的元素标记为一个组,并弹出这些元素。
- }
- }
完整代码:
[cpp] view plain copy
- #include <iostream>
- #include <string.h>
- #include <cstdio>
- #include <set>
- #include <algorithm>
- using
namespace std; - #define maxn 20100
- #define maxe 200100
- struct Edge
- {
- int v,next;
- }E[maxe];
- int dfn[maxn],low[maxn],head[maxn],Stack[maxn],Belong[maxn],parent[maxn],counter,len,Stop,n, MinVlaue,m,ans;
- void AddEdge(int a, int b)
- {
- len++;
- E[len].v = b;
- E[len].next = head[a];
- head[a] = len;
- }
- void dfs(int u)
- {
- int v;
- dfn = low=++counter; //初始化dfn与low
- Stack[Stop++]=u; //将u加入栈
- for (int i = head; i!=-1; i = E.next)
- {
- v = E.v;
- if (!dfn[v]) //节点v未被访问,则(u,v)为树边
- {
- parent[v]=u;
- dfs(v);
- low = min(low, low[v]);
- if(low[v]>dfn)
- {
- //printf("bridge: %d %d\n", u, v); // 该边是桥
- }
- }
- //节点v已访问,则(u,v)为回边
- else
if(v != parent) - {
- low = min(low, dfn[v]);
- }
- }
- if(low==dfn)
- {
- // 因为low == dfn,对(parent,u)来说有dfn > dfn[ parent ],因此low > dfn[ parent ]
- // 所以(parent,u)一定是一个桥,那么此时栈内在u之前入栈的点和u被该桥分割开
- // 则u和之后入栈的节点属于同一个组
- //将从u到栈顶所有的元素标记为一个组,并弹出这些元素。
- ans++;
- int temp=Stop-1;
- while (Stack[temp]!=u)
- {
- temp--;
- }
- MinVlaue=*min_element(Stack+temp, Stack+Stop);
- do
- {
- v=Stack[--Stop];
- Belong[v]=MinVlaue;
- }while (u!=v);
- }
- }
- int main()
- {
- int a,b;
- while (scanf("%d%d", &n, &m)!=EOF)
- {
- memset(head, -1, sizeof(head));
- memset(parent, 0, sizeof(parent));
- counter=0;
- ans=0;
- Stop=0;
- memset(dfn,0, sizeof(dfn));
- for (int i = 1; i <= m; i++)
- {
- scanf("%d%d", &a, &b);
- AddEdge(a,b);
- AddEdge(b,a);
- }
- dfs(1);
- printf("%d\n",ans);
- for (int i=1; i<=n; i++)
- {
- printf("%d ",Belong);
- }
- }
- return 0;
- }
|
|