上一篇最后提到要解决最优化问题 :<img alt="min_{(w,b)}" src="http://chart.apis.google.com/chart?cht=tx&chl=min_%7b%28w%2cb%29%7d%3cw%2cw%3e"> <img alt="s.t. y_i(+b) \geq 1" src="http://chart.apis.google.com/chart?cht=tx&chl=s.t.+y_i%28%3cw%2cx_i%3e%2bb%29+%5cgeq+1">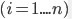
稍微对它做一下改动,如下:

 <img alt="y_i(+b) \geq 1" src="http://chart.apis.google.com/chart?cht=tx&chl=y_i%28%3cw%2cx_i%3e%2bb%29+%5cgeq+1"> <img alt="y_i(+b) \geq 1" src="http://chart.apis.google.com/chart?cht=tx&chl=y_i%28%3cw%2cx_i%3e%2bb%29+%5cgeq+1"> 
这是一个约束优化问题,更进一步说是一个二次规划问题,复习一下约束优化问题:
定义1:约束非线性问题是,

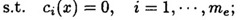
[url=http://images.cnblogs.com/cnblogs_com/vivounicorn/Windows-Live-Writer/SVM_B1AB/DK0CSF%7B%7E9Z80@60V0VNIYVK_2.jpg][img=240,23]http://images.cnblogs.com/cnblogs_com/vivounicorn/Windows-Live-Writer/SVM_B1AB/DK0CSF%7B%7E9Z80@60V0VNIYVK_thumb.jpg[/img][/url]
其中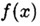 和 和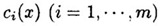 都是定义在 都是定义在 上的实值连续函数,且至少有一个是非线性的(反之为线性约束优化问题),m是一个正整数, 上的实值连续函数,且至少有一个是非线性的(反之为线性约束优化问题),m是一个正整数,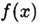 叫做目标函数, 叫做目标函数,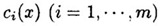 叫做约束函数,如果目标函数是二次函数则叫做二次规划问题,由同时满足所有约束方程的点组成的集合叫做可行域,这些点叫可行点。 叫做约束函数,如果目标函数是二次函数则叫做二次规划问题,由同时满足所有约束方程的点组成的集合叫做可行域,这些点叫可行点。 定义2:Farkas引理,对于给定的n维向量  与b,对于任意满足 与b,对于任意满足  的向量P,必有 的向量P,必有 的充要条件是:b在向量 的充要条件是:b在向量  所形成的凸锥内,即成立: 所形成的凸锥内,即成立: , ,  。 。 怎么理解“某个向量在若干其它向量形成的凸锥内”这个描述呢?可以看下图,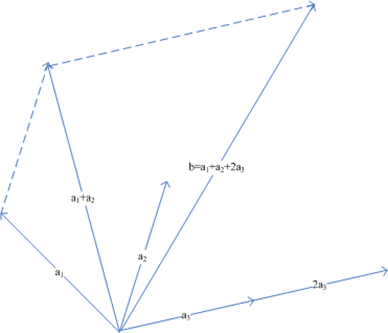 利用平行四边形法则,可以看到向量b处于由 形成的凸多边形内,发挥一下想象力,在空间中这不就像是一个凸的锥状体嘛。 形成的凸多边形内,发挥一下想象力,在空间中这不就像是一个凸的锥状体嘛。 定义3:对于约束问题,如果有一个可行点 ,存在 ,存在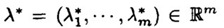 且满足 且满足 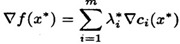  这里 这里 都是有效约束。 都是有效约束。 则 叫做K-T点。 叫做K-T点。 K-T点的几何意义可以从下图看出: 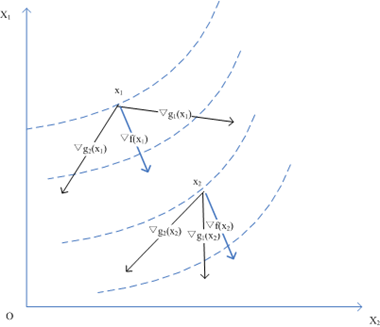
显然x1是K-T点而x2则不是。在一般非线性规划中,K-T条件是最优解的必要条件但不是它的充分条件,此时K-T点不一定是最优点,但对于凸规划问题,K-T条件是最优解的充要条件;顺便说下,凸规划是个好同志,它的局部最优解就是全局最优解,所以它的K-T点就是全局最优点。
|