定理1:设 是约束问题的局部极小点, 是约束问题的局部极小点, 点处的线性化可行方向的集合等于其序列可行化方向的集合,则必存在 点处的线性化可行方向的集合等于其序列可行化方向的集合,则必存在  使得: 使得: 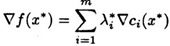 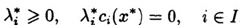 这里 这里 都是有效约束。 都是有效约束。 “ 点处的线性化可行方向的集合等于其序列可行化方向的集合”这个条件怎么满足呢?只要所有有效约束都是线性函数即可,此时 点处的线性化可行方向的集合等于其序列可行化方向的集合”这个条件怎么满足呢?只要所有有效约束都是线性函数即可,此时 必是一个K-T点。 必是一个K-T点。 定理2:一阶最优性条件:对于可行点 ,如果目标函数和所有有效约束在 ,如果目标函数和所有有效约束在 处可微,且任意、非零的,在 处可微,且任意、非零的,在 处的序列可行化方向向量d满足: 处的序列可行化方向向量d满足: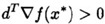 ,则 ,则 为严格局部极小点。这意味着,当向某一点处的任意方向移动都将导致目标函数值上升,那么这个点不就是一个局部极小点嘛。 为严格局部极小点。这意味着,当向某一点处的任意方向移动都将导致目标函数值上升,那么这个点不就是一个局部极小点嘛。 定理3:二阶最优性条件:设 为K-T点, 为K-T点, 是相应的拉格朗日乘子,如果 是相应的拉格朗日乘子,如果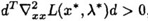 ,其中d为非零的、 ,其中d为非零的、 处的线性化零约束方向,则 处的线性化零约束方向,则 为严格的局部极小点。 为严格的局部极小点。 推论1:设 为K-T点, 为K-T点, 是相应的拉格朗日乘子,如果对一切满足 是相应的拉格朗日乘子,如果对一切满足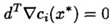 的非零向量d都有 的非零向量d都有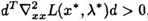 ,则 ,则 为严格的局部极小点。 为严格的局部极小点。
对于前面的约束非线性规划问题,如果 是二次函数且所有约束是线性函数的时候就变成了二次规划问题,这一写成以下形式: 是二次函数且所有约束是线性函数的时候就变成了二次规划问题,这一写成以下形式: 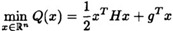 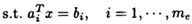 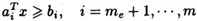 定理4:如果 是二次规划问题的可行点,则 是二次规划问题的可行点,则 是局部极小点的充要条件是:当且仅当存在拉格朗日乘子 是局部极小点的充要条件是:当且仅当存在拉格朗日乘子 ,使得: ,使得:   
 , ,
成立,(即 是K-T点)且对于一切满足 是K-T点)且对于一切满足 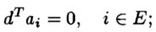 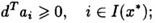 [url=http://images.cnblogs.com/cnblogs_com/vivounicorn/Windows-Live-Writer/SVM_B1AB/F%28YNGMII@Q9Y%28E%7DC6%7B1@KC5_2.jpg][img=240,27]http://images.cnblogs.com/cnblogs_com/vivounicorn/Windows-Live-Writer/SVM_B1AB/F%28YNGMII@Q9Y%28E%7DC6%7B1@KC5_thumb.jpg[/img][/url](其中E为等式的有效约束,I( )为不等式的有效约束) )为不等式的有效约束) 的向量d都有:0" src="http://chart.apis.google.com/chart?cht=tx&chl=d%5eTHd%3e0">。 |