0 引言
在电力电子工程的领域中,它是为各种电子控制设备服务的。凡是用晶闸管的地方,就要按设计者意图把它们组成一个功能线路。例如各种单相、三相、六相整流桥路,反并联线路,还有多支晶闸管的并联、串联应用线路等等。不同的应用,就有不同的线路,真可谓千变万化、不胜枚举。
在这样一个有独立功能的功率模块中,在通大电流工作时,其发热和散热是一对十分重要的矛盾,应用者应该了解其来龙去脉,妥善解决。否则会对整机可靠性造成重大影响。在一个2500A直流输出的三相全波整流桥工作时,这个单元自身发出的热量可高达约6KW数量级,如不及时把此热量散去,则后果不堪设想。
仅就风冷而言,散热所涉及的内容包括:散热器、风机、风道。而涉及的学科包括流体力学、传热学、材料学、风道结构设计等。
1 晶闸管的发热(功耗)原理
晶闸管自身功耗包括正向电流产生的功耗、开关损耗和反向漏电流损耗。在工频条件下使用开关损耗极小,漏电流损耗相对比重不大,约在一、二十瓦之内,故后两项不在本文中讨论。
1.1晶闸管的正向特性:
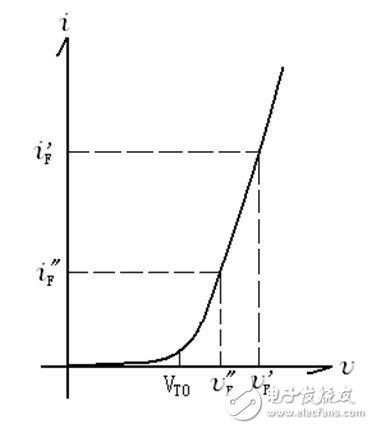
图1:晶闸管正向特性曲线
晶闸管正向特性曲线不是线性的,可近似看作两条直线组成:在电压VT0以前(即小于VT0时)晶闸管正向未能有效导通,电流极小;当电压大于VT0时,电流随电压上升,可看作一条直线,而且存在斜率,以斜率电阻rT0表示,单位为Ω(欧姆)。
图中曲线的函数关系为:

1.2晶闸管的正向功耗
正弦波时:
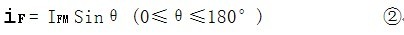
式②代入①,
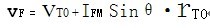
IFM为正弦波时的峰值电流,同样VFM可表示为正弦波的峰值电压。
正向平均电流:
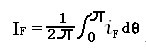
正向平均电压:
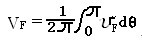
正向功耗:
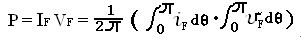
计算化简后:
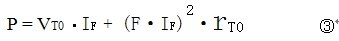
式中F为波形因子,随导通角而变。
在正弦波阻性负载时:

式中 IF·F=IF(RSM) ,IF(RSM)为正向电流有效值。因此在计算中可直接使用晶闸管的正向电流有效值。
由于晶闸管正向功耗P是由iF与vF乘积对0到180°角积分而得的,因此不是线性关系。用仪表测得的平均电流乘平均电压求功耗的方法是不对的。
在晶闸管产品说明书的参数表上都要列出每种规格晶闸管的VT0 和rT0 。
3 散热器热阻Rth(c-A)
散热器热阻可分为稳态热阻和瞬态热阻两种。
3.1热阻Rth的概念:
热阻是热导的倒数,单位是:℃/W (℃/瓦)具有温差的导热体两端存在热量由温高一端传到温低一端的现象。如温高一端发热功率为P,它们之间符合如下关系:

P是A端稳定产生的热功率。Rth 小时TA - TB 也小,即温差也小,反之温差也大。可见热阻小的导热体很快就能把热端热量传导出来。
散热器稳态热阻可以用经验公式计算近似值:
自冷条件下:

风冷条件下:

其中:l为散热器肋长; b为肋厚; L为散热器长; n为肋数;A为表面积; uS为风速;所用单位: l:米、A:米2、b:米、L:米、uS: 米/秒
肋长即为散热器翅片长
式中:a 取2.5;KS(铝)=140千卡/时·米·℃ ;KS(铜)=340千卡/时·米·℃
散热器热阻除了上述用经验公式计算外,一般由生产单位在样本上提供,也可通过实验测定(国标GB/T 8446.2-2004)。
3.2 稳态热阻
稳态热阻是指系统产生的热量与散去的热量相等时的热阻。此时,散热器上各点温度恒定,处于平衡状态。上面介绍的计算公式适用于稳态热阻。
3.3瞬态热阻
瞬态热阻表示的是热平衡建立前从受到热冲击起到建立热平衡(即各点温度恒定不变)止,散热器热阻值的变化的过程。热阻值是从小到大逐渐变的。从图四的曲线可知,起始的热阻值很小。这表明散热器不但能散热而且能吸收热量蓄热。吸收热量的过程也是散热器温度上升过程。吸热达到饱和时功耗和散热平衡,温度不再上升。这过程约20到40分钟左右。
晶闸管往往会用在存在大电流冲击(常称为浪涌电流)的电路中。如果浪涌电流时间只有几微秒到几秒,而且下一次浪涌到来前有较长时间的间隔,那么就可用瞬态热阻进行计算。在这种情况下散热器可大大缩小,甚至用足够热容量的铝板即可。
3.4热阻曲线
样本上提供的散热器热阻曲线如图三和图四所示。(也有用列表方式提供,如下表)

图2:稳态热阻曲线

图3:瞬态热阻曲线
图2是稳态热阻曲线。表示了该型号铝型材散热器在不同长度不同风速下的稳态热阻值。图3中左边曲线表示了该型号铝型材散热器瞬态热阻值。有了这样的热阻曲线,该型号散热器热阻值一查便知十分方便。
 |