摘要:选取电压模型为基础,引入参考值补偿策略保证电机在低速运行时可准确测得转子转速。硬件方面设计了由双DSP控制板和两电平逆变器组成的电机控制系统。在TMS320LF2407A和TMS320VC33组成的双DSP控制板中,TMS320VC33的高浮点计算能力解决了编程和计算精度的问题,利用TMS320LF2407A自身的硬件特点实现快速通信、采样等功能。
关键词:异步电机;传感器;矢量控制;磁通观测
1 引言
在高性能的异步电机矢量控制系统中,转速信息的获取必不可少。电机速度信息的辨识方法分为直接法和间接法。前者通过电子式或机电式速度传感器来获取电机速度信息,通常分为M法和T法来进行测速;后者通过测量电机的定子电流、定子电压等信号,根据电机的模型间接估计辨识电机的转速信息。然而由于速度传感器的安装给系统带来了如成本增加,易受干扰,适应性差,加大电机体积和轴向尺寸等问题,因此对无速度传感器转速估算方法的研究成为高性能交流调速的主要发展方向。使用无速度传感器控制方案,无需速度检测硬件,避免了速度传感器带来的诸多问题,提高了系统可靠性,降低了系统成本,同时,减小了系统体积和重量,减少了电机与控制器的连线,使采用无速度传感器的交流电机调速系统在工程中的应用更广泛。
2 控制原理
异步电机是一种多输入、多输出、非线性、强耦合系统,其稳态转矩表达式为:
Te=KITφmI2cosφ2 (1)
式中:KIT为与电机参数有关的常数;φm为电机气隙磁通有效值;I2cosφ2为电机转子电流有功分量。
由式(1)可见,感应电机的Te与定子电流无直接关系,并且电机的三相定子电流既要产生电机中的旋转磁场,又要产生电磁转矩,定子电流的激磁分量和转矩分量又与电机的设计情况和负载有关,很难将两者区分开。考虑到电机的动态过程,情况将更加复杂,因此异步电机要想将励磁电流和转矩电流分开比较困难,而矢量控制则解决了此问题。
由异步电机的数学模型出发,经过坐标变换,得到转子磁场定向坐标系中的异步电机模型。
定、转子电压、电流方程(标量形式)为:

整理转子d轴电压方程得到转子磁场定向下的磁链模型为:

由转子磁场定向磁链模型可见:ψr和定子电流d轴分量isd之间为一阶环节,其时间常数为转子时间常数。在稳态时,ψr的大小完全取决于isd的大小,控制isd即可获得所需的ψr。由式(3)可见,当ψr恒定时,Tem由定子电流q轴分量isq决定。控制isd,isq就可以独立地控制ψr和Tem从而实现二者解耦控制,使控制系统简化。
基于上述交流异步电机的无速度传感器矢量控制框图如图1所示。

图中检测的电机电流经过3/2变换,变换后isα,isβ为α,β坐标系下的电机定子电流。同时逆变器发出的电压usα,usβ进入磁链观测模块,isα,isβ同时进入旋转坐标变换模块得到同步旋转d,q坐标系下的电机定子电流isd,isq。isd进入磁链观测模块,通过磁链观测模块的计算得到估计的电机同步转速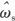 。给定磁链ψr*和给定的电机力矩电流isq*进入滑差计算模块得到滑差转速 。给定磁链ψr*和给定的电机力矩电流isq*进入滑差计算模块得到滑差转速 经减法器计算出转子转速再经过低通滤波器(LPF)滤波得到估计的转子转速 经减法器计算出转子转速再经过低通滤波器(LPF)滤波得到估计的转子转速 与给定转速ωr*经过减法器,再经过速度控制器输出指令电机转矩 与给定转速ωr*经过减法器,再经过速度控制器输出指令电机转矩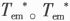 经过转矩电流计算模块,计算出isq*。ψr*经过磁场计算模块计算出给定的电机磁场电流isd*。isq*与检测的电机力矩电流isq进入减法器,再经电流控制器产生给定的电机力矩电压。isd*与检测的电机磁场电流isd进入减法器,再经电流控制器产生给定的电机磁场电压。给定的电机力矩电压和给定的电机磁场电压分别加上补偿电压,进入旋转变换模块,通过电压变换模块,施加到三相感应电机上。 经过转矩电流计算模块,计算出isq*。ψr*经过磁场计算模块计算出给定的电机磁场电流isd*。isq*与检测的电机力矩电流isq进入减法器,再经电流控制器产生给定的电机力矩电压。isd*与检测的电机磁场电流isd进入减法器,再经电流控制器产生给定的电机磁场电压。给定的电机力矩电压和给定的电机磁场电压分别加上补偿电压,进入旋转变换模块,通过电压变换模块,施加到三相感应电机上。
根据上述分析,要想实现转子磁场定向控制,必须知道转子磁链;另外由转速计算公式可知,要想计算转速,也必须观测磁链,知道了磁链角度就可计算同步频率和转矩电流,用转矩电流和转子磁链幅值可计算滑差频率,同步频率减去滑差频率就可得到转速。因此,要实现无速度传感器矢量控制,首先要准确观测磁链。
3 磁链观测
静止坐标系中的电压型转子磁链模型为:

电压模型可以根据加在电机上的电压与电机电流经过积分计算估计出转子磁链。该模型框图如图2所示。

电压型转子磁链观测模型高速性能较好,但在低速时因为电机产生的反电动势较小,检测信号的信噪比较低,在此基础上计算得到的转子磁链不太准确,而且存在积分器漂移问题。
该问题解决方案为将输出结果再通过一个高通滤波器s/(s+ωc)将低频成份和直流漂移滤掉。

式中:ωc为截止频率;x为系统输入;y为系统输出;1/s为纯积分环节。
由式(8)可知,纯积分和一阶高通滤波的组合可等效为一阶惯性环节。但高通滤波器的引入带来了磁链检测的幅值和相位的误差。为了补偿磁链的幅值和相位变化,同时还要使积分稳定,在此采用了以下改进方法。 以滞后环节1/(s+ω)代替纯积分环节,并引入转子磁链参考值ψr*作为幅值和相位误差的补偿,从而得到一种改进的电压型转子磁链观测模型如图3所示。

在参数准确的情况下,实际磁链ψr=er/s,观测磁链可表示为:

式中:er为转子产生的反电动势,er=Lr(us-Rsis-Lσpis)/Lm。
可见,在参数准确情况下,如果ψr*=ψr,式(9)右边第2项为零,于是有 ,所以改进型电压模型可以做到无幅值和相位误差。因此,这种改进型电压转子磁链观测模型可以在极低速的情况下得出比较准确的转子磁链观测结果。另外,当TL取为转子时间常数Tr时,由电机的定子电阻参数误差带来的磁链相位误差可以在低速时降到一个很低的水平。 ,所以改进型电压模型可以做到无幅值和相位误差。因此,这种改进型电压转子磁链观测模型可以在极低速的情况下得出比较准确的转子磁链观测结果。另外,当TL取为转子时间常数Tr时,由电机的定子电阻参数误差带来的磁链相位误差可以在低速时降到一个很低的水平。
改进型电压模型的反电势输入端经过的不是纯积分环节,故在实际应用中没有纯积分环节的初值和漂移问题。该方法还有一个特点:当滤波时间常数ω取为与Tr相等时,观测磁链的角度在零转速附近对定子电阻的误差有鲁棒性。
4 硬件构成
双DSP数字化开发平台控制板以TMS320VC33作为系统的计算核心,TMS320LF2407A作为系统的控制核心,两个DSP处理器之间通过双口RAM
进行数据交换,并采用CPLD为程序存储器、数据存储器以及I/O口进行地址译码和读写控制。
5 试验
利用试验来验证所提出的无速度传感器矢量控制测速方法的正确性。其中试验电机参数:额定功率2.2 kW,额定线电压380V,额定电流为5 A,额定频率为50 Hz,额定转速为l 420 r·min-1,极对数为2,定子电阻2.54 Ω,定子漏感11.6279mH,转子电阻1.798 Ω,转子漏感11.627 9 mH,励磁电阻3.91 Ω,励磁电感235.071 8 mH。

图4为滤波前后估计同步转速 与转速ωs波形。滤波后 与转速ωs波形。滤波后 =31.423 9 rad·s-1,ωs=30.230 8 rad·s-1。转差为1.193 1 rad·s-1。同步转速给定为5 Hz转换为角速度31.415 9 rad·s-1。同步转速估计误差为0.292 rad·s-1,相对误差0.93%。图5示出转速5 Hz时实际转速和估计转速对比。由图可知,在转子频率5Hz时,电角度为62.8rad·s-1,估计转速误差最大为0.68rad·s-1,相对误差为1.08%。 =31.423 9 rad·s-1,ωs=30.230 8 rad·s-1。转差为1.193 1 rad·s-1。同步转速给定为5 Hz转换为角速度31.415 9 rad·s-1。同步转速估计误差为0.292 rad·s-1,相对误差0.93%。图5示出转速5 Hz时实际转速和估计转速对比。由图可知,在转子频率5Hz时,电角度为62.8rad·s-1,估计转速误差最大为0.68rad·s-1,相对误差为1.08%。
6 结论
采用TMS320LF2407A和TMS320VC33组成的双DSP系统为硬件基础,基本思想是利用改进型电压模型,实现同积分运算等效的幅值和相位特性。电机稳态工作时,转子反电动势信号是正弦波形。而一个频率为ω的理想正弦信号在经过积分环节运算后,输出相位滞后π/2,幅值变为原来的1/ω倍。
从试验中可知,观测得到的磁链与转子反电动势信号在输出相位上与通过纯积分环节得到的相位仍有一点偏差,故还需要对补偿环节上进行进一步研究,如何使其补偿相位完全等效于积分的效果。由试验结果可见,5 Hz时的转速估算误差很低,验证了所提理论的正确性。 |