Java 容器源码分析之 Deque 与 ArrayDeque(2)
|
 
- UID
- 1066743
|

Java 容器源码分析之 Deque 与 ArrayDeque(2)
底层结构1
2
3
4
5
6
7
8
| //用数组存储元素
transient Object[] elements; // non-private to simplify nested class access
//头部元素的索引
transient int head;
//尾部下一个将要被加入的元素的索引
transient int tail;
//最小容量,必须为2的幂次方
private static final int MIN_INITIAL_CAPACITY = 8;
|
在 ArrayDeque 底部是使用数组存储元素,同时还使用了两个索引来表征当前数组的状态,分别是 head 和 tail。head 是头部元素的索引,但注意 tail 不是尾部元素的索引,而是尾部元素的下一位,即下一个将要被加入的元素的索引。
初始化ArrayDeque 提供了三个构造方法,分别是默认容量,指定容量及依据给定的集合中的元素进行创建。默认容量为16。
1
2
3
4
5
6
7
8
9
10
11
12
| public ArrayDeque() {
elements = new Object[16];
}
public ArrayDeque(int numElements) {
allocateElements(numElements);
}
public ArrayDeque(Collection<? extends E> c) {
allocateElements(c.size());
addAll(c);
}
|
ArrayDeque 对数组的大小(即队列的容量)有特殊的要求,必须是 2^n。通过 allocateElements方法计算初始容量:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| private void allocateElements(int numElements) {
int initialCapacity = MIN_INITIAL_CAPACITY;
// Find the best power of two to hold elements.
// Tests "<=" because arrays aren't kept full.
if (numElements >= initialCapacity) {
initialCapacity = numElements;
initialCapacity |= (initialCapacity >>> 1);
initialCapacity |= (initialCapacity >>> 2);
initialCapacity |= (initialCapacity >>> 4);
initialCapacity |= (initialCapacity >>> 8);
initialCapacity |= (initialCapacity >>> 16);
initialCapacity++;
if (initialCapacity < 0) // Too many elements, must back off
initialCapacity >>>= 1;// Good luck allocating 2 ^ 30 elements
}
elements = new Object[initialCapacity];
}
|
>>>是无符号右移操作,|是位或操作,经过五次右移和位或操作可以保证得到大小为2^k-1的数。看一下这个例子:
1
2
3
4
| 0 0 0 0 1 ? ? ? ? ? //n
0 0 0 0 1 1 ? ? ? ? //n |= n >>> 1;
0 0 0 0 1 1 1 1 ? ? //n |= n >>> 2;
0 0 0 0 1 1 1 1 1 1 //n |= n >>> 4;
|
在进行5次位移操作和位或操作后就可以得到2^k-1,最后加1即可。这个实现还是很巧妙的。
添加元素向末尾添加元素:
1
2
3
4
5
6
7
8
9
10
11
| public void addLast(E e) {
if (e == null)
throw new NullPointerException();
//tail 中保存的是即将加入末尾的元素的索引
elements[tail] = e;
//tail 向后移动一位
//把数组当作环形的,越界后到0索引
if ( (tail = (tail + 1) & (elements.length - 1)) == head)
//tail 和 head相遇,空间用尽,需要扩容
doubleCapacity();
}
|
这段代码中,(tail = (tail + 1) & (elements.length - 1)) == head这句有点难以理解。其实,在 ArrayDeque 中数组是当作环形来使用的,索引0看作是紧挨着索引(length-1)之后的。参考下面的图片:
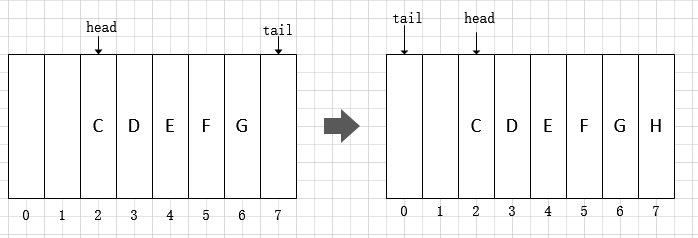
那么为什么(tail + 1) & (elements.length - 1)就能保证按照环形取得正确的下一个索引值呢?这就和前面说到的 ArrayDeque 对容量的特殊要求有关了。下面对其正确性加以验证:
1
2
3
4
5
| length = 2^n,二进制表示为: 第 n 位为1,低位 (n-1位) 全为0
length - 1 = 2^n-1,二进制表示为:低位(n-1位)全为1
如果 tail + 1 <= length - 1,则位与后低 (n-1) 位保持不变,高位全为0
如果 tail + 1 = length,则位与后低 n 全为0,高位也全为0,结果为 0
|
可见,在容量保证为 2^n 的情况下,仅仅通过位与操作就可以完成环形索引的计算,而不需要进行边界的判断,在实现上更为高效。
向头部添加元素的代码如下:
1
2
3
4
5
6
7
| public void addFirst(E e) {
if (e == null) //不支持值为null的元素
throw new NullPointerException();
elements[head = (head - 1) & (elements.length - 1)] = e;
if (head == tail)
doubleCapacity();
}
|
其它的诸如add,offer,offerFirst,offerLast等方法都是基于上面这两个方法实现的,不再赘述。 |
|
|
|
|
|