2.3 硬币直径检测
通过光电传感器实现硬币直径及通过币道的加速度的检测。如图3,在币道的A点、B点和C点分别安装光电收发器。AB点和BC点的距离相等且为s。
硬币通过币道时做匀加速度运动,设加速度为a,下面通过由FPGA高速检测得到的ta,tb,tc以及光电传感器之间的距离s来求加速度a,并求出硬币的直径d。
设硬币的前沿通过A点,B点,C点的速度分别为vA,vB,vc,则有:
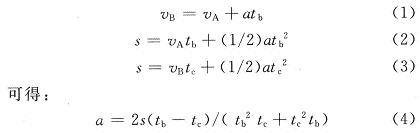
由此可计算出硬币通过币道时的加速度a。设光电传感器A距离币道底部的垂直距离为h;光电传感器A检测点扫过硬币的长度为l。图5为硬币的半径r和h,l的关系图。由图5可得如下公式:
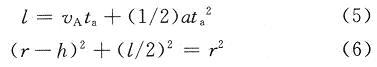
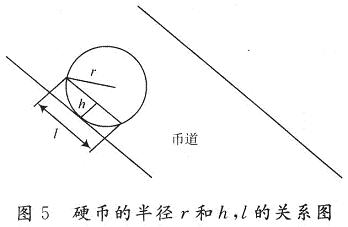
硬币的直径为d=2r,由式(1)~式(6)可得:
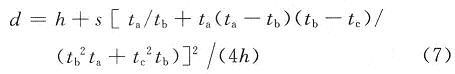
式中:h和s是已知的;ta,tb,tc可通过FPGA检测得到。
由此公式,就可通过测量硬币通过的时间ta,tb,tc并计算得到硬币的直径d。
2.4 等距离多点采样
见图3,D,E点位置设在检测线圈的边缘,CD间的距离为s。当硬币前沿通过D点时,开始采样;当硬币后沿通过E点时,停止采样。为了充分地采集硬币在各个位置的参数信息,采样点应足够多。在本设计中,沿硬币滚动的方向每间隔0.1 mm位移采样一次。
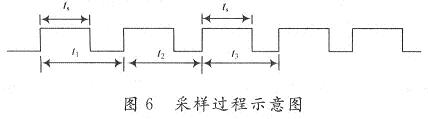
检测线圈和检测电路组成振荡器,振荡频率既不能太高,也不能太低。在本设计中,振荡频率为200 kHz(此频率指硬币未通过线圈时的振荡频率)。经实际测试,硬币通过检测线圈时的速度范围为0.1~0.5 m/s。可见,硬币通过币道时的速度有较大的变化范围,同一硬币多次投币时,通过检测线圈同一点(比如:A点)的速度也有区别。为了实现每次投币多点采样时,检测线圈和硬币的相对位置都一样,就必须采取等位移多点采样。当硬币的前沿通过D点时开始采样,以硬币前沿通过D点的时刻作为采样时间的零起始时刻,每过0.1 mm采样一次。首先,需要计算出通过每一个0.1 mm位移所需要的时间t1,t2,t3,…。由于速度越来越快,必定有t1,>t2>t3>…,再每隔t1,t2,t3,…时间检测采样一次。图6为采样过程示意图,tS为采样时间。
由于硬币在币道中做匀加速度直线运动,设硬币的前沿通过D点时的速度为vD,则有:
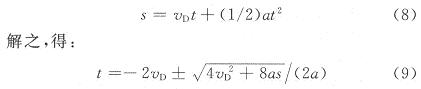 令s为0.1 mm,0.2 mm,0.3 mm,…,设需要的时间分别为t0.1,t0.2,t0.3,…。由2.3所述方法可求得a和vD,则通过求解一元二次方程可得到t0.1,t0.2, t0.3,…,若以硬币通过D点作为零时间参考点,则在t0.1,t0.2,t0.3,…采样即可得到正确的等位移多采样值。有:t1=t0.2-t0. 1,t2=t0.3-t0.2,…。
当硬币后沿通过E点时,停止采样,D点和E点的沿币道方向的距离为y,设通过E点的时刻为tE,则有:
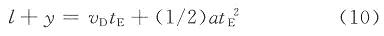
由此即可计算出tE,即为硬币通过币道时最后一个采样点。
根据式(9),要求得t,涉及到开方运算。开方运算的算法主要有Newton-Raphson算法、SRT-Redun-ant算法和Non-Redudant算法。这三种算法可以得到开方运算的近似结果。关于上述三种算法的介绍参见参考文献[1—3]。
为了有足够高的检测精度,要求t精确到1μs。另外,由于硬币由C点到D点的最小时间为0.3 ms,所以必须在0.3 ms内完成上述的算法。通过FPGA不难实现这些要求,但是若采用单片机来实现就有一定的难度,如:若用51单片机,频率12 MHz来实现,则机器周期就是1μs,要实现上述算法是不可能的。所以在该设计中采用FPGA实现。
2.5 基于FPGA的多倍周期同步测频法
在该设计中,检测线圈为电涡流反射式互补检测,准确地测试出其输出频率是很重要的。对于频率的测试,有测频法、测周期法,但测量精度都不够高,在该设计中,两种测试方法误差都比较大,所以采用等精度多倍周期同步测频法,可达到较高的精度。
由于硬币通过检测线圈时的速度范围为:0.1~0.5 m/s,要求每隔0.1 mm距离采样一次,则采样的时间间隔范围为0.2~1ms。为了保证采样的快速和准确性,采样时间不能超过0.2 ms,本设计采样时间取0.1 ms。
该设计中,FPGA的频率为100 MHz,由检测线圈及检测电路组成的振荡器频率为200 kHz(此频率指硬币未通过线圈时的振荡频率)。
所谓测频法,就是先给定一个闸门时间,在此闸门时间内,对被测频率信号计数,由此即可计算出被测信号的频率。在本设计中,闸门时间为0.1 ms,被测信号频率为200 kHz左右,若用测频法,则测量误差为:
1/(0.1×10-3×200×103)=5%
所谓测周期法,就是在被测频率信号的一个周期内,对参考频率信号进行计数,由此即可计算出被测信号的周期,在本设计中,参考频率信号为100 MHz,被测信号频率为200 kHz左右,若用测周期法,则测量误差为:
(200×103)/(100×106)=0.2%
由此可见,都有较大的误差,下面用等精度多倍周期同步测频法,既可以在振荡频率变化的情况下保持精度的一致,又可以减少测量误差,提高测试精度。
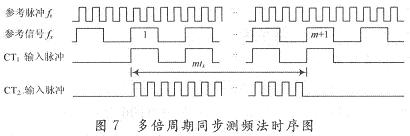
设被测信号频率为fx,计数器CT1对fx进行计数;参考信号频率为fr,计数器CT2对fr进行计数。
CT1的闸门开放时间完全与fx的m个周期同步。闸门开放时间T1=mtx。在fx的第一个上升沿和第m+1个上升沿之间的mtx时间间隔内,允许CT2对fr计数,计数值记为N。上述测频的时序图如图7所示。
fx的计算公式如下:
fx=m/Nfr
根据误差传递公式,有:
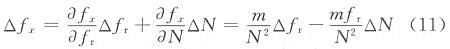
式中:△fx,△fr,△N为绝对误差。相对误差δ=±(△fx/fx),由于fr由晶体振荡器输出,其稳定度较高,所以△fr非常小,可忽略不计。△N极限是±1,故测量误差δ为:
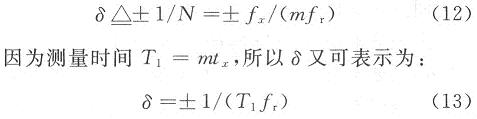
由式(13)可以看出,测量误差与被测信号的频率大小无关,仅与闸门时间和标准频率时间有关。标准频率越高,闸门时间越长,测量误差越小。
在本设计中,为了保证测量的速度,闸门时间比较短,在闸门时间不变的情况下,标准频率越高,误差越小。
为了提高测量频率的精度,必须采用较高频率的标准信号。在传统的硬币识别器设计中,多采用单片机测量频率,但由于单片机受本身的时钟频率和若干指令运算的限制,难以得到较高的标准频率信号,无法满足高速、高精度的测量要求。采用高速、高精度、高可靠性的现场可编程阵列FPGA为实现高速、高精度的测频提供了保证。
在本设计中,fr=100 MHz,T1=0.1 ms,则相对测量误差δ为:
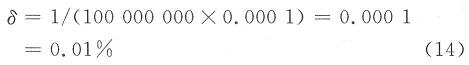
误差远小于测频法和测周期法误差。这就解决了瞬时、快速采样的测量精度问题。
若用传统的单片机等精度多倍同步测频方案,假设用常用的MCS-51单片机,设时钟频率为12 MHz,机器周期为1 MHz,则误差为:
δ1=1/(1 000 000×0.000 1)=0.01=1%(15)
可见,用传统的单片机采集频率数据,误差太大,难以满足高精度测量的要求。
正是出于提高测量精度的考虑,在本设计里用了FPGA来完成频率数据的采集工作。
3 结 语
在硬币识别器的研究中,本文首先提出了基于FP-GA的等位移多点采样法,并且提出基于FPGA 的光电检测来对硬币的直径进行准确测量的方法,具有一定的理论指导意义和较强的实际应用价值。通过这些方法,大大提高了硬币识别的准确性和可靠性,特别是在对硬币的制造材料不均匀的情况下,更能体现其优越性。笔者曾对国外大公司,如:日本的GLORY公司、美国A&A公司生产的硬币识别器进行研究,由于其在硬币识别方面为单点采样法,所以其对一些不均匀硬币(如:泰国的10铢硬币)识别效果并不理想,由于本硬币识别器采取等位移多点采样法,所以识别效果较好,识别准确率可达到99.5%以上。另外,硬币识别器在某些情况下,需要在比较恶劣的环境下使用,需要较强的抗干扰能力,如:在野外使用的投币电话,在公共汽车上使用的无人值守投币机。由于FPGA的纯硬件电路特性,抗干扰能力特别强,具有很高的可靠性。 |