摘要：设计了一种基于双级矩阵变换器(TSMC)驱动的永磁同步电机(PMSM)滑模变结构直接转矩控制方案。该方案针对一般滑模控制器的抖振问题，设计了积分滑模面、符号函数平滑和变指数趋近律，并应用于PMSM转矩和磁链的控制，既克服了滞环直接转矩控制(DTC)转矩和磁链脉动大的不足，又解决了一般滑模控制器的抖振问题。采用DSP和FPGA开发了一套系统实验样机，给出了系统的软硬件设计方法，实验结果验证了系统设计的有效性，实现了系统高性能调速及网侧电能质量的优化。
关键词：永磁同步电机；矩阵变换器；滑模控制；直接转矩控制
1 引言
矩阵变换器作为一种理想“全硅”型变换器，具有无直流储能环节，输入功率因数可调，输出电压大小、相位和频率可调等优点。TSMC在保留上述优点的同时，还具有换流方法简单，逆变级可采用成熟的SVM算法等特点，故可方便地应用于高性能伺服控制系统中。
PMSM具有结构简单，效率高，功率密度高等优点，应用场合广泛。DTC作为高性能控制策略被广泛应用在PMSM控制中。但传统DTC存在电流、磁链和转矩脉动大，低速运行难以精确控制等不足。针对上述问题，国内外学者作了许多关于DTC改进的研究。
为了既能实现PMSM较好的传动性能，又能满足日益严格的电网电能质量要求，这里将TSMC和DTC各自优点相结合，设计开发了一套基于TS MC的PMSM DTC系统。采用一种变指数趋近率滑模控制器和SVM矢量控制方法代替传统滞环控制器和开关表。滑模控制器迫使磁链和转矩进入设定的滑模面，大大减小了脉动，SVM控制器产生TSMC逆变端调制信号。
2 永磁同步电机数学模型
在PMSM建模与分析、设计过程中常做以下假设：转子永磁磁场在气隙空间分布为正弦波，定子电枢绕组中的感应电动势也为正弦波，忽略定子铁心饱和，认为磁路为线性，电感参数不变；不计铁心涡流与磁滞损耗；转子上无阻尼绕组。
基于上述假设，建立d，q坐标系下的PMSM数学模型，其电压方程为：
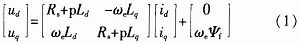
式中：ud，uq，id，iq，Ld，Lq为d，g轴电压、电流、电感；Rs为定子电阻；ωe为转子电角速度；p为微分算子；ψf为永磁体磁链。
磁链和电磁转矩方程为：
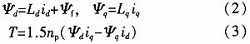
式中：np为电机的极对数。
3 变指数滑模控制器的设计
3．1 变指数滑模趋近率
为克服指数趋近率切换带为带状，系统最终不能趋近于原点的缺点，对其做出进一步改进，得出一种新的变指数趋近率：
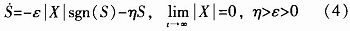
变指数趋近率让系统状态量开始时以变速和指数两种速率趋向滑模面，当接近滑模面时，指数项接近零，-ε|X|S变速项起关键作用。当选取的状态量X在系统稳定过程中无限趋近于零时，滑模控制律的作用让X进入滑模面并向原点运动，此过程又让控制律中的控制项-ε|X|S不断减小，最终稳定于原点。为进一步消弱到达原点前状态变量运动轨迹的抖振，符号函数采用平滑处理为：
sgn(S)=S／(|S|+σ) (5)
式中：σ为一个数值较小的正常数。
3．2 滑模控制器设计
选择如下积分滑模面：
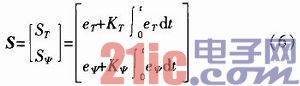
式中：eT为转矩估算值与给定值的误差，eT=T*-T；eψ为磁链估算值与给定值的误差，eψ=ψ*-ψ；ST为转矩滑模面；Sψ为磁链滑模面。
PMSM的变指数趋近率为：
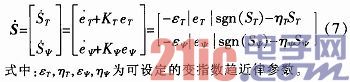 在滑模面以外的运动中，系统运动点呈指数方式向滑模面运动，当接近滑模面时，系统进入切换带，穿越滑模面的运动与误差的绝对值|e|成比例，则幅值会越来越小，理想情况下最终会稳定到原点，误差为零，导致抖振的滑模切换项sgn(S)消失，抖振消除：
控制律中重要且关键的是B的求逆，由于系统开始运行时无法保证B的奇异性，会出现求不出其逆矩阵的情况。解决方法是每次求逆前先判断矩阵的奇异性，满足非奇异条件时求逆，不满足时则保持上一次的运算结果。
4 滑模变指数TSMC-PMSM调速系统
图1为TSMC-PMSM调速系统原理框图。采用DTC策略，转矩和磁链采用上述设计的控制器，转速外环采用PI控制器。内环控制器的输出ud，uq经2r／3s变换得ua，ub，uc，它们作为TSMC逆变级调制策略的参考给定，通过TSMC调制产生驱动PMSM定子侧三相电压。
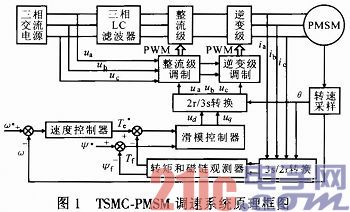
TSMC整流级采用PWM，逆变级采用SVM：
(1)整流级PWM 为保持在中间直流上正下负的同时，尽可能充分地利用三相输入线电压，以合成较大的直流电压，将三相正弦输入相电压ua，ub，uc划分为6个区间。图2为整流级分区。
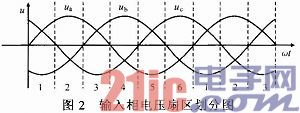
以1扇区为例，在一个调制周期内保持ub持续导通。ua，uc占空比为：
D1=ua／(-ub)，D2=uc／(-ub) (15)
类似容易得到其他区段的占空比计算公式。
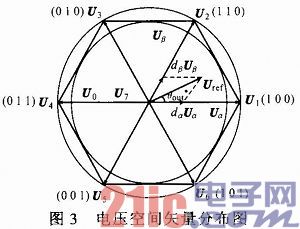
(2)逆变级SVM 逆变级采用SVM技术，电压空间矢量分布图如图3所示，平面被分为6个区间。假定参考空间矢量Uref位于区间1，Dm，Dn，Do分别为U1，U2和零矢量的占空比。对于TSMC，由于整流级与逆变级没有大电容连接，为了与整流级协调以满足零电流换流，通常逆变级分为两段调制，占空比为：
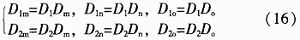
5 系统设计及实验
TSMC驱动系统的全数字化实现得益于现代微处理器，特别是专用DSP及全控型功率器件，尤其是智能功率模块(IPM)的问世。系统硬件部分主要由控制板、TSMC主电路和驱动电路及为驱动电路供电的电源、电压电流采样电路及光电编码盘速度和位置检测部分、滤波电路、保护电路、PMSM等组成。
控制电路主要由TMS320F28335型DSP和EP2C8T144C8N型FPGA组成，其中FPGA主要根据TSMC整流级和逆变级的调制时间(占空比乘以调制周期)产生TSMC的驱动脉冲，即完成了TSMC的调制，同时FPGA还负责TSMC的保护功能；而基于滑模变结构的PMSM的DTC算法及TSMC占空比计算则由DSP完成，同时DSP还负责与上位机进行串口通信。
TSMC主电路由整流级、箝位电路以及逆变级构成。逆变级由PM75RLA120型IPM组成的通用逆变器构成，其自带驱动电路，极大地简化了驱动电路的设计。整流级由12个分立式1MBH60D-100型IGBT构成，共发射极连接构成双向开关。采用集成驱动芯片M57962驱动。此系统软件程序流程图如图4所示。
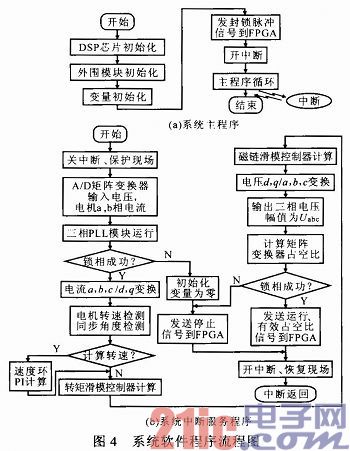
系统控制对象PMSM参数为：额定电压220 V；额定电流3．2 A；额定转速3 000 r·min-1；定子电阻2．4 Ω；直轴电感8．62mH；交轴电感10．5mH；极对数为2。系统TSMC输入端滤波电感大小为0．8mH；滤波电容为30μF；开关频率为10kHz。通过实验得到波形如图5，6所示。
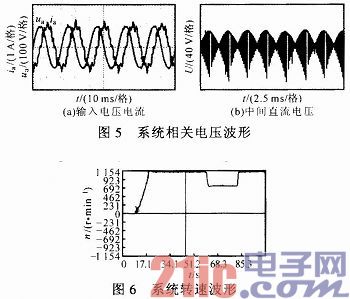
图5a为TSMC整流级输入a相电压电流波形。由图可见，此时电压相位超前电流，这是由TSMC输入端滤波器呈容性所致，但超前相位较小，输出侧基本呈单位功率因数。图5b为闭环调速时TSMC中间直流电压波形。图6为实际转速波形。实验过程中，系统初始转速给定为零，在10 s时刻转速给定切换为1 125 r·min-1，在60 s时刻转速给定切换为750 r·rain-1，之后在80 s时切换回1 125 r·min-1。由图可见，系统在转速突变时动态响应很快，稳态转速误差小，无抖振，具有较强的鲁棒性。
6 结论
这里设计了一种基于双级矩阵变换器的永磁同步电机滑模变结构直接转矩控制方案。该控制方法克服了滞环直接转矩控制中转矩和磁链脉动大的不足。针对一般滑模控制器的抖振问题，设计了积分滑模面、符号函数平滑和变指数趋近率，解决了滑模变结构固有的抖振问题。设计并实现了实验样机，实验结果验证了永磁同步电机的高性能调速，同时网侧基本实现了单位功率因数，达到了很好的实验效果。 |
