|
 
- UID
- 864567
|

摘要:为了估算锂离子动力电池的荷电状态(SOC), 在对影响SOC 值的因素及传统SOC 估算方法分析的基础上,依据实际情况,采用了一种新思路,即将电池的工作状况分为静止、恢复、充放电三种状态,分别对三种状态进行SOC 估算。在估算过程中分散并消除影响SOC 值的因素,特别在充放电状态下,使用了以库仑效率因子为基础的电量的动态恢复量对安时计量法进行改进,解决了安时计量法会产生累积误差的问题。经实验表 明,此方法提高了电池SOC 计算的精度,达到了动力汽车的应用要求。
锂电池已被广泛应用于工业、日常生活等领域,对 电池荷电状态(SOC)的估算已成为电池管理的重要环节。但是,由于电池结构复杂,电池的荷电状态受放电电流、电池内部温度、自放电、老化等因素的影响, 使得SOC的估算困难。目前SOC估算方法有:开路电压法、安时计量法、内阻法、神经网络和 卡尔曼滤波法。国外V. Pop等人提出EMF-SOC模型[1-2],即电池电动势与荷电状态的关系模型来估算SOC,相当于开路电压法,该方法用于电池静置足够长时间后进行估 计,不能实时估计;也有人采用安时计量法或卡尔曼滤波法估计SOC,安时计量法由于电流波动较大或测量误 差长时间积累导致估计不精确;卡尔曼滤波法则在建立准确实用的电池动态模型上存在很大困难,为此本文根据锂电池在应用中的实际情况,采用了一种新思路来估 算SOC,即将电池的工作状况分为三种状态,对每种状态的SOC逐一进行估算,在估算过程中消除影响SOC的因素,且使三种状态下SOC的值互为前提,从 而提高SOC的估算精度。
1、电池工作状态及SOC估计
电池状态根据实际情况可分为三种状态,这里将其定义为静止、恢复、充放电,它们的关系如图1。
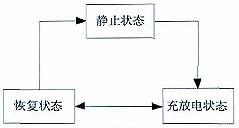 图1 电池工作状态图
1.1 静止状态
电池的静止状态是指电池工作停止后,完全恢复了的状态,从恢复状态转化而来,可直接转入充放电状态,此状态下SOC的计算量作为充放电状态下SOC估算 的初始值。由于此状态下的特点是电流为零、无极化现象,其SOC值与开路电压有很好的对应关系,因此能用开路电压法直接估算电池的SOC值,电池的开路电 压与SOC值的关系曲线如图2。
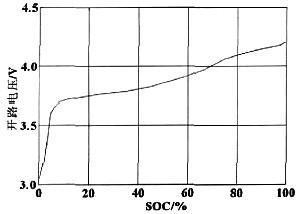 图2 电池的开路电压与SOC值的关系曲线
在静止状态下,电池容量主要受自放电现象的影响使得电池电量会随着时间的增加而减少,而用开路电压与SOC值的对应关系来估算SOC,本身就可以消除自放电引起的电量损失的影响,从而能使SOC值更加准确地反映电池的状态。
1.2 恢复状态
恢复状态是指电池从放电或充电状态转到静止状态的过渡阶段。一般这个阶段经历的时间为8h(此值为经验值),此状态下SOC的计算量作为充放电状态下 SOC估算的初始值,这时的SOC估算主要考虑放电或充电结束后电池电量的改变量。从放电或充电状态进入恢复状态后电池电量会随时间增加而有所增加,其变 化的原因是在放电或充电过程中电池内部产生极化现象,部分电量没有用于实际的充放电中而是慢慢累积起来,当电池停止工作后极化现象会慢慢消失,累积的电量 也会恢复。
恢复阶段SOC的估算:
(a)若从放电状态进入恢复状态
SOCt=SOCd+M×t/(8×Q)×100%
式中:SOCt为恢复状态下的荷电状态值;SOCd为放电状态终止时的荷电状态值;M为在电池放电过程中的累积电量(可以恢复);t为电池在恢复状态下经历的时间;Q为电池的实际容量。
(b)若从充电状态进入恢复状态
SOCt=SOCc+M×t/(8×Q)×100%
式中:SOCt为恢复状态下的荷电状态值;SOCc为充电状态终止时的荷电状态值;M为在电池充电过程中的累积电量(可以恢复);t为电池在恢复状态下经历的时间;Q为电池的实际容量。
M值的计算:
(a)放电状态下
若η2>η1,
Mt+Δt=Mt+I2×Δt×(1-η2)/η2-I1×Δt×(η2-η1)/η1×η2(1)
推导如下:
t+Δt时刻,安时计量法计算的电量:I2×Δt;
t+Δt 时刻,电池实际放出的电量:I2×Δt/η2;
t+Δt时刻,电池损失电量:I2×Δt ×(1-η2)/η2;
t时刻,I1放电时,由于η2>η1,损失电量I1×Δt×(1-η1)/η1较大,在t+Δt 时刻就会恢复少许电量,恢复量为:
I1×Δt×(1-η1)/η1-I1×Δt×(1-η2)/η2
即I1×Δt ×(η2-η1)/η1×η2
若η1≥η2,t+Δt时刻损失的电量更大,因此就无恢复量I1×Δt ×(η2-η1)/η1×η2.
Mt +Δt=Mt+I2×Δt ×(1-η2)/η2 (2)。
式中:η1、I1为电池在t时刻的放电库仑效率和电流,η2、I2为电池在t +Δt 时刻的放电库仑效率和电流。
(b)充电状态下,充电方式一般为恒流恒压方式,因此库仑效率、电流值的变化较放电状态下稳定。
恒流阶段,电流恒定,而电池温度会有所增加:
M t +Δt=Mt+I×Δt ×(1+η1-2η2)
公式推导同(1)。
式中:I为恒流阶段的电流值;η1、η2为恒流阶段的充电库伦效率,η2>η1,它们的差别是由温度引起的。恒压阶段,电流会随电压的升高而降低。
若η2>η1,Mt +Δt=Mt+I2×Δt×(1-η2)-I1×Δt ×(η2-η1)公式推导同(1)。
若η1≥η2,Mt+Δt=Mt+I2×Δt×(1-η2)公式推导同(2)。
式中:η1、I1为电池在t时刻的充电库仑效率和电流;η2、I2为电池在t +Δt 时刻的充电库仑效率和电流。
在充电情况下,一般用已规定好的电流进行充电,可认为η=1. |
|