作者:jbb0523(彬彬有礼)
本文共说明了以下问题:
一、在matlab中如何表示频率为f1,以采样率f抽样后所得到的数字信号?如此表示的依据是什么?
二、使用matlab画出的频谱(一般是幅度谱或称振幅谱)的横坐标轴的意义是什么?如何根据横坐标轴的值得到其所对应的实际频率?
三、实数序列的频谱除第零个点和第N/2个(当N为偶数时)点外(从0~N-1),其它具有共轭对称性质;复数序列呢?
四、频率分辨率指的是什么?高分辨谱和高密度谱有何区别?有何作用?
约定:对于信号cos(wt),它是以周期为2*pi/w为周期的信号,角频率w=2*pi*f,我们经常这样称呼这个信号:它的角频率为w,频率为f Hz,周期T=1/f秒;
1)在matlab中对信号s1(t)=cos(w1t)=cos(2*pi*f1*t)进行采样,其中f1=1000Hz,根据奈奎斯特采样定理,采样频率f>=2*f1,在此我们取f=3000Hz。
在matlab中仿真也好,实际中处理的信号也罢,一般都是数字信号。而采样就是将信号数字化的一个过程,设将信号s1(t)数字化得到信号[url=]s1(n)=cos(2*pi*f1/f*n)[/url],其中n=[0…N-1],N为采样点数。
我们来解释一下s1(n),为什么说s1(n)=cos(2*pi*f1/f*n)表示以采样率f对频率为f1的信号进行采样的结果呢?采样,顾名思义,就是对信号隔一段时间取一个值,而隔的这段时间就是采样间隔,取其倒数就是采样率了,那们我们看s1(n)=cos(2*pi*f1/f*n),将前面的参数代入,当n=0时,s1(0)=cos(0),当n=1时,s1(1)=cos(2*pi*1000/3000*1),当n=2时, s1(2)=cos(2*pi*1000/3000*2),当n=3时,s1(3)=cos(2*pi*1000/3000*3),这是不是想当于对信号s1(t)的一个周期内采了三个样点呢?对一个频率为1000Hz的信号每周期采三个样点不就是相当于以3倍于频率的采样率进行采样呢?注意,当n=3时相当于下一个周期的起始了。
我们取采样点数N=64,即对64/3=21.3个周期,共计64/3/f1=21.3ms时长。
我们在matlab中输入以下命令:
[url=]>> n=0:63;[/url]
>> f1=1000;f=3000;
>> s1=cos(2*pi*f1/f*n);
>> plot(abs(fft(s1)));
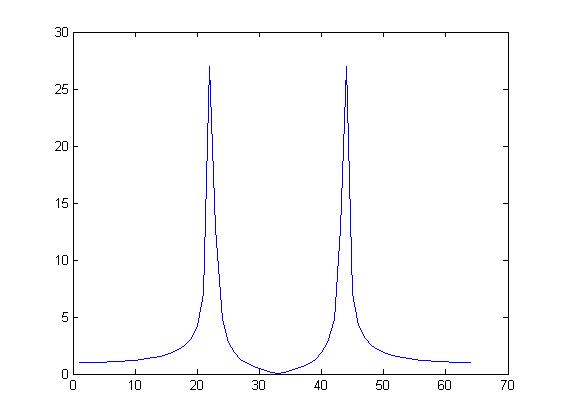
图1 我们对图1进行一下解释,以说明图中的横坐标轴的所代表的意义。
对于信号[url=]s1(t)=cos(w1*t)[/url],我们知道它的傅里叶变换是S1(w)=pi*[url=][[/url]δ(w-w1)+δ(w+w1)]。
如果在[url=]-2*pi*3000/2~2*pi*3000/2[/url]范围内观察信号s1(t)的频谱,则应该在[url=]+2*pi*1000[/url]和-2*pi*1000两个频点上有两根谱线,而对采样后的数字信号,频率坐标轴范围-2*pi*3000/2~2*pi*3000/2将被归一化到-2*pi*(3000/2)/3000~2*pi*(3000/2)/3000即-pi~pi范围内,因此将在+2*pi*1000/3000和-2*pi*1000/3000即+2*pi/3和-2*pi/3的两个频点上有两根谱线。注意,此时坐标轴上的2*pi代表着3000Hz的频率范围。
另外还有一点应该明白的是,时域采样意味着频域的周期延拓,即-pi~pi上的谱线与[url=]-pi+M*2pi~+pi+M*2pi[/url]范围内的谱线是一模一样的,其中M为任意的整数。更通俗的说,a~b之间的频谱与a+M*2pi~b+M*2pi之间的频谱是一模一样的。因此-pi~0之间的频谱与pi*2pi之间的频谱是一样的。
在matlab中,如果仅简单的执行plot绘图命令,坐标横轴将是1~N,那么这1~N代表着什么呢?是的,应该代表0*2pi,应用到上面的例子即是0~3000Hz的频率范围。
其中1~N/2代表0~pi,而N/2~N代表-pi~0。
从理论上讲s1(t)=cos(2*pi*f1*t)应该在1000Hz和-1000Hz两个频点上有两根线,即应该在x1(其中x1*(3000/2) /(64/2)=1000,解得x1=21.3)上和64-x1上有两根谱线。观察图1可知,两个峰值大约对应横轴坐标为21和43=64-21两个点。
若令s2(t)=sin(w1*t),则傅里叶变换是S1(w)=-j*pi*[url=][[/url]δ(w-w1)-δ(w+w1)],在matlab中执行以下命令:
[url=]>> n=0:63;[/url]
>> f1=1000;f=3000;
>> s2=sin(2*pi*f1/f*n);
>> plot(abs(fft(s2)));
则可得其频谱,如图2所示:

图2 由图可得两个峰值的位置基本与图1相同,这由其傅里叶表达式也可以得出此结论。
以上分别说明了余弦和正弦的频谱,而且余弦和正弦均是实数序列,实数序列的离散傅里叶变换(DFT)具有共轭对称性质(此性质可百度或查阅数字信号处理相关书籍或自行推导,很简单的),这从图中也可以看出。(画图时取其模值,共轭取模与原先数取模将变成相等)
2)复数的频谱
若令[url=]s3(t)=cos(w1*t)+j*sin(w1*t)[/url],则计算其傅里叶变换可得S2(w)=pi*[δ(w-w1)+δ(w+w1)]+j*{-j*pi*[δ(w-w1)-δ(w+w1)]}=2*pi*δ(w-w1),因此频谱中将只有一根谱线。
在matlab中输入以下命令:
[url=]>>[/url] n=0:63;
>> f1=1000;f=3000;
>> s3=cos(2*pi*f1/f*n)+1j*sin(2*pi*f1/f*n);
>> plot(abs(fft(s3)));
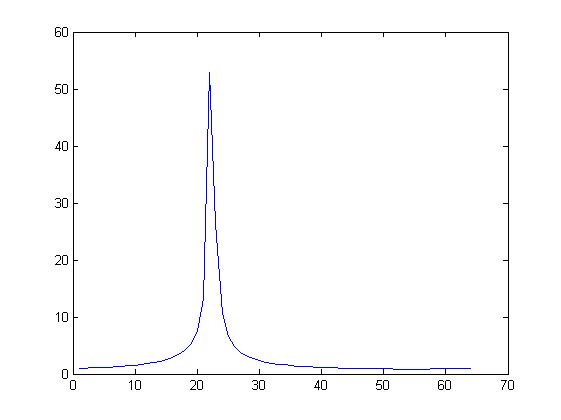
图3 从图3可以看出,对于一个复数序列求频谱,它的幅度谱将不再是对称的两根谱线。其实经过类似于实数序列的推导可以得出,复数序列的频谱将不再具有类似于实数序列的共轭对称性质。
当w1为负值时会如何呢?输入以下命令计算s4(t)=cos(w1*t)+j*sin(w1*t)的频谱:
[url=]>> n=0:63;[/url]
[url=]>> f1=-1000;f=3000;[/url]
>> s4=cos(2*pi*f1/f*n)+1j*sin(2*pi*f1/f*n);
>> plot(abs(fft(s4)));
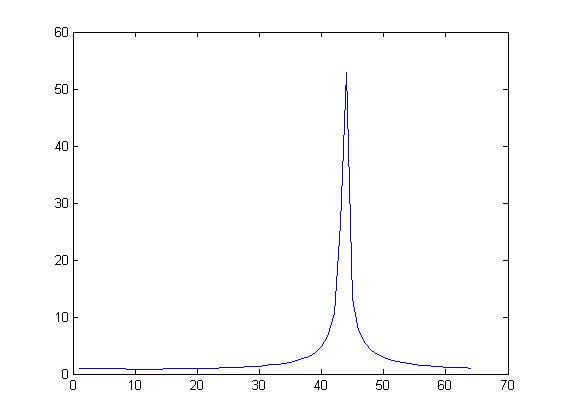
图4 对比图3和图4可知,当频率为正值时,峰值将在1~32范围内;而当频率为负值时,峰值将在33~64之间。此性质可通俗的描述如下:
对于信号s(t)=cos(2*pi*f*t)+j*sin(2*pi*f*t),对其进行符合奈奎斯特采样定理的采样,设采样率为fs,采样点数为N,得到数字信号s(n),n=[0,…,N-1],则对s(n)做DFT变换进行谱分析后得到S(k),k=[0,…,N-1]。观察S(k)的幅度谱,若k=0~N/2-1之间有峰值,则s(t)的频率f在0~fs/2之间;若k=N/2~N-1之间有峰值,则s(t)的频率f在-fs/2~0之间;并且有且只有一个峰值。
计算公式如下:设幅度谱峰值当k=k1时出现,则s(t)的频率为:
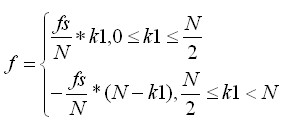
同理,可推出如下性质:
对于信号s(t)=cos(2*pi*f*t)-j*sin(2*pi*f*t),对其进行符合奈奎斯特采样定理的采样,设采样率为fs,采样点数为N,得到数字信号s(n),n=[0,…,N-1],则对s(n)做DFT变换进行谱分析后得到S(k),k=[0,…,N-1]。观察S(k)的幅度谱,若k=0~N/2-1之间有峰值,则s(t)的频率f在-fs/2~0之间;若k=N/2~N-1之间有峰值,则s(t)的频率f在0~fs/2之间;并且有且只有一个峰值。
计算公式如下:设幅度谱峰值当k=k1时出现,则s(t)的频率为:
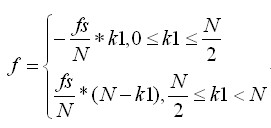
3)下面引入一个新的概念:频率分辨率
频率分辩率是指频域取样中两相邻点间的频率间隔。更确切的说是如果某一信号含有两个频率成分f1和f2,Of=|f2-f1|,频率分辨率的概念是如果频率分辨率大于Of,对信号进行谱分析后将不能视别出其含有两个频率成分,这两个频率将混叠在一起。
以下是摘自华科姚天任《数字信号处理(第二版)》第92页的一段:

现在我们设定信号s5(t)=cos(w1*t)+sin(w2*t),其中w1=2*pi*1000,w2=2*pi*1100
在matlab中输入以下命令计算其频谱:
[url=]>> n=0:63;[/url]
[url=]>> f1=1000;f2=1100;f=3000;[/url]
>> s5=cos(2*pi*f1/f*n)+sin(2*pi*f2/f*n);
>> plot(abs(fft(s5)));
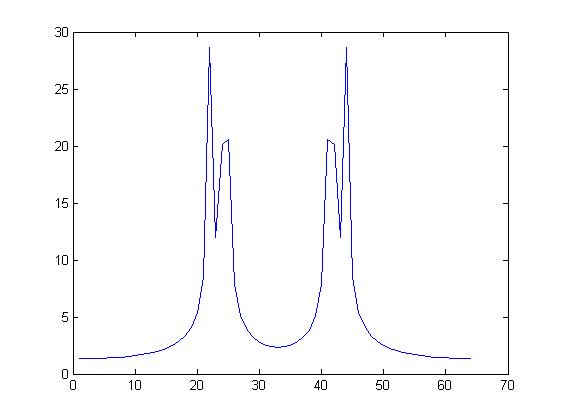
图5
从图5中可以看出能够分辨出f1=1000Hz和f2=1100Hz两个频率分量。
我们利用上面的理论来计算一下此时的频率分辨率:
采样频率fs=3000Hz
采样点个数N=64
最长记录长度tp=N*(1/fs)
频率分辨率F=1/tp=fs/N=3000/64=46.875Hz
因为F<f2-f1=100Hz,因此能够分辨出两个频率分量。
下面我们作如下尝试:
第一种尝试:fs不变仍为3000Hz,即奈奎斯特定理仍然满足,[url=]大于信号[/url]s5(t)的最高频率分量1100Hz的两倍,但将采样点个数N减小为24个,在matlab中输入以下命令:
[url=]>> n=0:23;[/url]
>> f1=1000;f2=1100;f=3000;
>> s5=cos(2*pi*f1/f*n)+sin(2*pi*f2/f*n);
>> plot(abs(fft(s5)));
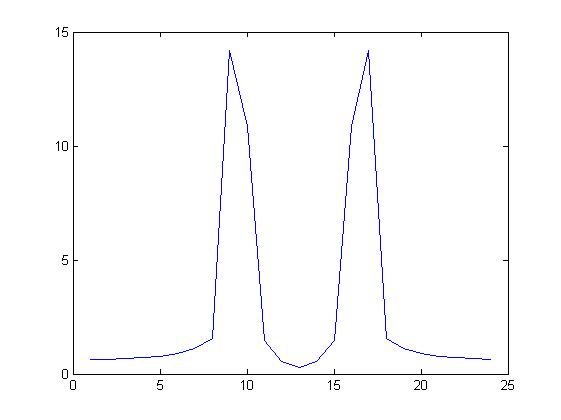
图6
第二种尝试:采样率fs升为8000Hz,即满足奈奎斯特采样定理,大于信号s5(t)的最高频率分量1100Hz的两倍,采样点个数N不变,仍为64个,在matlab中输入以下命令:
[url=]>> n=0:63;[/url]
>> f1=1000;f2=1100;f=8000;
>> s5=cos(2*pi*f1/f*n)+sin(2*pi*f2/f*n);
>> plot(abs(fft(s5)));

图7 由图6和图7可以看出,这两种尝试虽然满足奈奎斯特采样定理,但都不能分辨出两个频率分量,用前面的理论知识可以作如下分析:
第一种尝试的频率分辨率F=1/tp=fs/N=3000/24=125Hz>100Hz
第二种尝试的频率分辨率F=1/tp=fs/N=8000/64=125Hz>100Hz
因此以上两种尝试均不能分辨出频率间隔为100Hz的两个频率分量。
4)最后我们引用高密度谱的概念,如图6所示,频谱很不平滑,呈很明显的折线状态,我们在matlab中输入以下命令:
[url=]>> n=0:23;[/url]
>> f1=1000;f2=1100;f=3000;
>> s5=cos(2*pi*f1/f*n)+sin(2*pi*f2/f*n);
>> plot(abs(fft([s5,zeros(1,104)])));
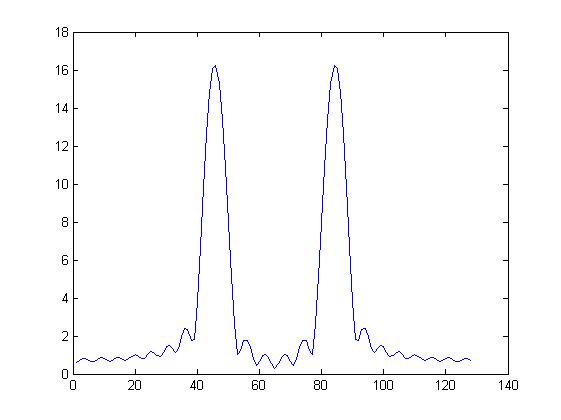
图8 图8是将图6中的信号在时域补了104个零后才进行谱分析的。比较图6与图8,虽然相对于图6来说图8的频率分辨率并没有增加,但其每个点所代表的频率更小了,也就是密度更高了(同样3000Hz的频率,图6中使用了24点,而图8中使用了128点),这就是高密度谱。通常可以靠补零的方式来提高频谱的密度,但补零不能提高频率分辨率。很多人在此很迷惑,在末尾加零后,使一个周期内的点数增加,必然使样点间隔更近,谱线更密,事以前看不到的谱分量就可以看到了,能够看到更多的谱,不是提高分辨力了吗?其实加零后,并没有改变原有记录的数据,原有数据的频谱一开始就存在,我们只是有的看不见,加零后只是让我们看见原来本就存在的频率,也就是说,原始数据代表的该有的频率就有,没有的频率加再多的零(极限是成连续的),也没法看见。
在数字信号处理中,高分辨率谱和高密度谱是较为易混淆的两个概念。获得高分辨率谱的途径是增加信号采样的记录时间tp,而高密度谱则是通过在时域补零得到的。高分辨谱的用途很显示,可以分辨出频率间隔更小的两个频率分量,那么高分辨率谱有什么作用呢?要想明白高密度谱的概念,就不得知道一个名词:栅栏效应。高分辨率谱就是为了减小栅栏效效的。实际信号是无限长的,其频谱是连续的,但是要用计算机对信号进行频谱分析,就必须把它截短使之成为有限长度为tp的信号,这样的截短相当于对信号加矩形窗。经过加窗截取,信号的周期变为tp,其频谱相应地由原来的连续谱变为离散谱,离散谱的谱线只在f=1/tp的整数倍的位置上才出现,于是谱线间的实际信号的谱线有可能被挡住而损失掉,这称之为栅栏效应。例如截取信号长度为tp=0.5s,则可得到的谱线为2Hz,4Hz,6Hz,8Hz,…,若信号中包含频率为7Hz的分量,则该分量将被栅栏挡住,无法显示出来。
参考文献: 【1】姚天任.数字信号处理(第二版)[M].华中科技大学出版社,2000. 【2】万灵达.基于FFT的高精度频率估计算法研究[D].西安电子科技大学,2010. 【3】其它网络资源. | 
