当你看到标题时,可能会问,FFT有什么好讨论的,难道ZDS2022示波器的FFT功能会有什么本质上的不同吗?我们不妨简单地回顾一下FFT中几个重要的参数和关系表达式。
采样率:示波器的采样频率,用Fs表示。ZDS2022示波器每通道均支持1GS/S采样率,下面将以最高采样率1GS/S为基准描述相关的问题;
FFT点数:示波器用于FFT变换的样本数据个数,用N表示。ZDS2022示波器最大可以执行4M点的实时FFT运算。显然用400万个点做FFT,势必需要相当惊人的运算能力和运算效率;
频率分辨率:用△f 表示示波器最小能分辨多小的频率。假设频率分辨率为10Hz,则可分辨10Hz、20Hz、30Hz……等10Hz整数倍的频率点,但不能分辨出15Hz、25Hz、37Hz等非整数倍的频率点。
如果被测信号中存在15Hz这样的信号,显然经过FFT变换后,频谱上不能出现15Hz这个频率点,即无法分析出来。但该频点的能量将泄露到旁边相近的10Hz 和20Hz 频点上,不仅造成15Hz的信号分辨不出来,则连10Hz和20Hz频点的幅值也不准确,因为15Hz频点的能量泄露到这几个频点上去了。因此唯有进一步提高频率分辨率,比如,提高到5Hz或1Hz或更高(△f值更低越好)。当采样率一定时,则只能通过增加FFT点数才能提高频率分辨率,其前提是示波器要有足够的运算能力,且有足够的存储深度,即两者缺一不可。另一种办法是降低采样率,则势必导致无法分析高频信号,在某些情况下并不允许,而且除非是售价几十万和上百万的示波器,一般都无法手动调整示波器的采样频率。
采样时间:在采样率Fs下,采集N个点所需要的时间,用T表示,显然T=N / Fs。注意该采样时间对应于FFT变换所用的N个点,而非整个示波器的捕获时间。而示波器捕获时间对应于整个存储深度,当做FFT变换时,并不一定需要使用全部的存储深度,因此两者不等价。

图 1 ZDS2022示波器
事实上,上述FFT中的参数构成了一个重要关系式,将贯穿整个关于FFT的阐述之中。
△f = Fs / N (1)
即频率分辨率等于采样率除以FFT点数。将上述公式稍作变换:
△f = Fs / N = 1 / (N / Fs) = 1 / T (2)
即频率分辨率等于采样时间的倒数。实际上公式(1)和(2)是等价的,只是从不同的角度来说明问题而已。
为什么示波器必须做到4兆点的实时FFT呢?常见的一些示波器,FFT最大只支持8K个点,甚至有些示波器只有1K个点。根据上面的关系表达式可以看出,在1GS/S采样率下,最高频率分辨率只有
Fs/N=1GS/S / 8K点 = 125KHz
也就意味着,如果被测信号不是125K的整数倍,则根本无法判断信号频谱。真实世界能有多少个被测信号正好是125KHz整数倍的呢? 因此这种示波器的FFT没有任何实用价值。这也是为什么在其它示波器的宣传资料中,几乎见不到关于FFT性能宣传的根本原因。
由于致远电子对FFT做了大量的深度优化,使得ZDS2022示波器最大可以支持4M点FFT。根据上述的关系表达式,在1GS/S采样率下,FFT的频率分辨率达到了1GS/S / 4M点 = 250Hz。显然,在1GS/S采样率条件下示波器能够达到这样的频率分辨率,也就是说只要被测信号频率是250Hz的整数倍,ZDS2022仍能准确无误地分辨出来。即便被测信号不是250Hz的整数倍,此时存在频谱泄露,但在250Hz这么小的频率分辨率下,也能较准确地分析出被测信号的大致频点。
假设被测信号中包含100KHz和150KHz两种频率分量,以及其它的一些更高频率的信号,对于普通示波器来说,由于最大只支持8K点FFT,即频率分辨率只有125KHz,显然无法分辨出100KHz和150KHz频点信号。为了证明这一点,我们不妨做一些测试。为了避免真实信号中本身的干扰影响到分析的准确性,则采用MATLAB构建一个纯正的信号来从数学原理上进行分析。假设设计一个信号:
y = 0.7*sin(2*pi*100000*t) + 1.2*sin(2*pi*150000*t)
这是一个包含100KHz和150KHz两种频率分量的信号,幅值分别为0.7和1.2,此信号详见下图:
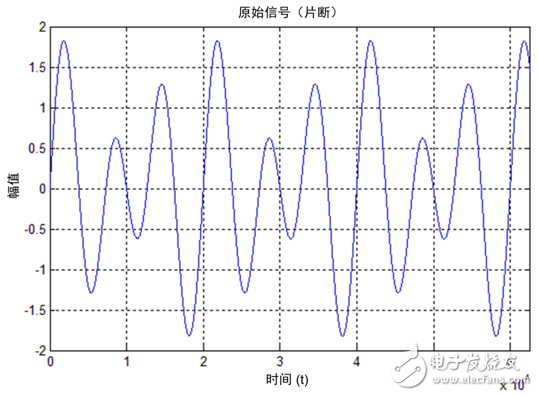
图2 原始信号(包含100KHz和150KHz两种频率分量)
本文选自电子发烧友网11月《测试测量特刊》Change The World栏目,转载请注明出处!
 下面分别以1GS/S采样率对该信号采样,计算8K点和4M点的FFT,此处直接给出结果,其相应的代码详见程序清单。

图3 程序清单Matlab代码
按理说FFT可以直接分析出100KHz和150KHz频率信号,真的是这样?如下图所示为8K点FFT结果,为何没有看到100KHz和150KHz这两个信号呢?而屏幕上只有一个125KHz的信号,且幅值既不是0.7,也不是1.2,却是毫不相干的1.464。因为在8K点时,频率分辨率只有Fs/N=1GS/S / 8K = 125KHz,这无法分辨100KHz和150KHz频点同时由于频谱泄露,250KHz频点处都能看到幅值为0.2249,直流分量(0Hz)也有幅值0.2062,显然给出的信号并无这两个分量。那么8K点FFT给了用户正确结果吗?没有。不单是幅值不正确,就连那些最基本的频率分量都是错的,这样的FFT有何意义?

图4 8K点FFT结果
下面再来看一下4M点FFT得出的结果将会是怎样,详见下图。由于4M点FFT时频率分辨率高达250Hz,因此可以准确无误地分辨出100KHz和150KHz频点信号,且无频谱泄露,100KHz信号幅值为0.7,150KHz信号幅值为1.2,准确无误地给了用户最真实的结果,4M点相对8K点的FFT优势在此一览无余。

图5 4M点FFT结果
假设经常要分析电路中存在的噪声,如果示波器的频率分辨率不够细,则无论如何都无法准确定位噪声来源。如果采用ZDS2022示波器进行分析,由于ZDS2022示波器在4M点FFT、1GS/S采样率下频率分辨率仍能达到250Hz,则经过FFT后就能准确地发现20KHz的噪声。联想到所用的DC-DC开关频率正好是20KHz的,在这种测试场合下,ZDS2022示波器能够迅速定位噪声来源。
综上所述,其实解决用户的麻烦就是创新的机会,当在200MHz带宽示波器上实现了4M点的FFT运算时,在1GS/s采样率下FFT的频率分辨率仍达到了250Hz水平,示波器就一定能真正地成为信号分析的利器。因此对于工程师来说,千万不能小看个人的力量,只要给我们一个支点就一定有可能撬动地球。致远电子技术创新的故事告诉我们,只要注重细节用心做事,世界一定会因为我们而不同。 |