|
 
- UID
- 852722
|

引言
ZigBee技术中定义了3种设备:协调器(Coordinator),路由器(Router)和终端设备(EndDevice)。协调器主要负责启动整个网络;路由器的功能主要是允许其他设备加入网络及多跳路由等;终端设备一般没有特定的维持网络结构的责任。ZigBee技术通过这3种设备可以构成一个移动自组织的网络,广泛应用在家庭、环境监测、工农业等场合[1]。目前的定位技术总体上可以分为基于测距技术与无需测距技术。前者定位精度较高,后者实现起来比较简单。在测距技术中,有基于接收信号强度(RSSI)、基于到达时间差(TOA)、基于不同波的到达时间差(TDOA)以及到达角度差(AOA)等[24]。在这几种测距技术中,基于RSSI的测距技术将接收到的信号强度转换为节点之间的距离,不需要额外的硬件和数据交换,有成本低、容易实现等优点。本文结合CC2430/CC2431芯片,设计了一种基于RSSI的测距定位算法。
1 RSSI测距的实现原理
基于RSSI的测距技术是利用无线电信号随距离增大而有规律地衰减的原理来测量节点间的距离的。接收信号强度RSSI与传输距离d的关系如下所示[5,8]:RSSI=-(10×n×lgd+A)(1)式中,n表示信号传播常数,也叫传播系数;d表示与发送者的距离;A表示距发送者1 m时的信号强度。测距精度的高低受到n与A实际取值大小的影响较大。A是一个经验参数,可以通过测量距离发送者1 m处的RSSI 值得到。n是用来描述信号强度随距离增加而递减的参量,n的大小依赖具体的环境。为了得到最优的n值,可以先放置好所有的参考节点,然后尝试用不同的n_index值找到最适合这个具体环境的n值。
2 节点组成的定位网络
2.1 CC2430/CC2431芯片介绍
CC2430/CC2431是Chipcon公司(现被TI收购)推出的针对IEEE 802.15.4/ZigBee应用的片上系统,其内部集成了工作在24 GHz的射频收发器,拥有低功耗的8051 MCU内核、128 KB可编程Flash ROM和8 KB RAM,还有A/D转换器、定时器等。另外,CC2431片上系统由CC2430加上Motorola公司基于IEEE 802.15.4标准的无线定位引擎组成。其定位引擎支持3~l6个参考节点的定位运算,最高精度可达05 m;定位时间少于40 μs,定位区域为64 m×64 m,定位误差为3~5 m,与一般软件定位相比,具有定位速度快、定位准确度高、消耗CPU资源少的特点[6]。
CC2430/CC2431主要外围电路图如图1所示。
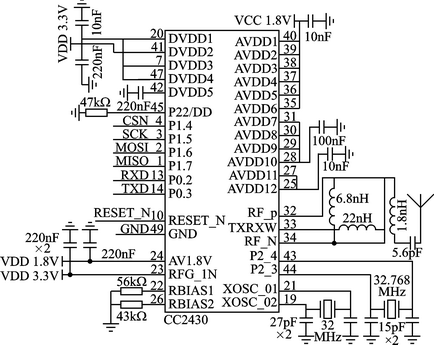
图1 CC2430/CC2431主要外围电路图
2.2 节点构成的定位网络

图2 ZigBee定位网络控制界面
ZigBee网络中有一类节点作为协调器,通过串口负责与PC通信;还有一类节点是参考节点,如图2中周边的4个圆圈,地址分别为0x143E、0x0001、0x3CB8、0x287B。这4个节点坐标已知,中间的圆圈(地址0x0002)为盲节点。盲节点可以根据接收信号强度,选取其中3个信号强度比较强的参考节点,采用三边测量法估算出盲节点的坐标位置。如图2所示,盲节点实时显示的坐标为(6.25 m,5.75 m)。
图3为CC2431定位引擎的定位流程。
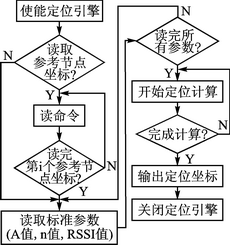
图3 CC2431定位引擎的定位流程
2.3 最小二乘法修正距离
从式(1)可以看出,如果知道参考节点与盲节点之间的RSSI值,则可以估算出两个节点之间的距离。然而不同的环境下可能存在不同的信号干扰,采用节点之间的RSSI值估算距离必然存在一定的误差。这时可以根据特定的环境对测量到的距离采用传统的最小二乘法进行修正[7]。得到修正后的距离,从而可以更加精确地估算出盲节点的坐标。具体步骤如下:
① 根据实际情况布置好节点,参考节点(Mi,Ni)与盲节点(Mj,Nj)的位置坐标均已知。可以根据xi=(Mi-Mj)2+(Ni-Nj)2得到实际节点之间的距离。
② 根据式(1)估算出盲节点与各个参考节点之间的距离yi。
③ 采用最小二乘法拟合实际距离xi与估计距离yi的关系。假设两者之间的关系为yi=axi+b,为了使所有数据偏差的平方和很小,假设R2=∑mi=1(yi-axi-b)2。可以把R2看作自变量a和b的二元函数,要使得R2最小,分别对自变量求导,令其等于零。
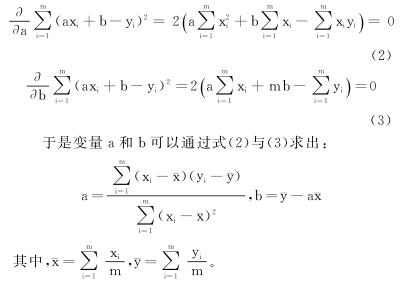
根据得到的a与b的值可以拟合出修正距离与估计距离的关系Y修=a×X估+b,结合式(1)可以得到:
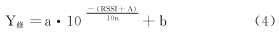
④ 布置盲节点,通过式(1)估计盲节点与参考节点之间的距离x,通过第3步拟合好的修正距离与估计距离之间的关系修正估计距离,得到修正的距离Y修。
2.4 盲节点坐标估计
选择3个接收信号强度最强的参考节点,采用三边测量法估计出盲节点坐标值[8]。假设3个参考节点A、B、C的坐标分别为(ma,na)、(mb,nb)、(mc,nc),盲节点E的坐标(m,n)未知。通过2.3节4个步骤得到盲节点与3个参考节点的修正距离分别为da、db、dc。则根据两点之间的距离公式可以得到式(5):
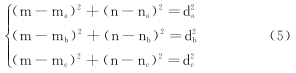
展开并化简,可得到盲节点E的坐标(m,n),如式(6)所示:
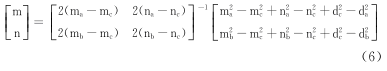
3 实验结果分析
在35 m×35 m的区域内布置4个参考节点,定位网络控制界面如图2所示。通过采集100个数据包,经过重复调整,n取16、A取47时定位效果最好。通过最小二乘法拟合出修正距离与估算距离之间的关系,得到a=1058 1,b=0193 4。因此,根据式(4)可以得到修正距离与估计距离之间的关系Y修=10581×10-(RSSI+A)10n+0193 4。修正前与修正后的测距值如表1所列,修正前与修正后盲节点坐标估计误差如表2所列。
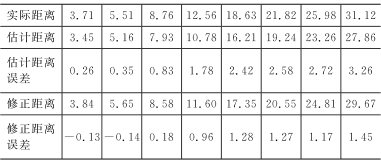
表1 修正前与修正后的测距值m
从表1中可以看出,相比于修正前的估计距离,经过最小二乘法修正后的距离更加接近于实际距离,误差更小,从而能更加精确地估算出盲节点的坐标。从表2中可以看出,经过修正后的距离采用三边测量法估算出盲节点的坐标误差要小于修正前的坐标估算误差。
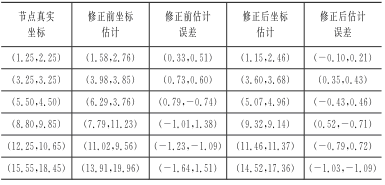
表2 修正前与修正后盲节点坐标估计误差m
结语
ZigBee技术是一门新兴的学科,在生活中的各个领域都有重要的作用,定位算法是ZigBee技术中的重要算法之一。本文简要分析了RSSI测距原理,在此基础上结合最小二乘法原理,对估算的距离进行修正,并在以CC2430/CC2431为核心设计的ZigBee节点上组网实验。实验表明经过修正后的距离精度更高,对盲节点的坐标定位更加精确,修正后的定位精度符合一些常规的定位系统要求。 |
|