|
 
- UID
- 1029342
- 性别
- 男
|

维特比算法(Viterbi Algorithm)(2)

某病人连续三天就诊,医生了解到第一天她感觉是normal, 第二天是cold, 第三天是dizzy。医生的疑问是:最能解释对病人的这些观察值的健康状态序列是什么?这个问题可以通过维特比算法来回答。
def viterbi(obs, states, start_p, trans_p, emit_p): V = [{}] path = {} # Initialize base cases (t == 0) for y in states: V[0][y] = start_p[y] * emit_p[y][obs[0]] path[y] = [y] # Run Viterbi for t > 0 for t in range(1, len(obs)): V.append({}) newpath = {} for y in states: (prob, state) = max((V[t-1][y0] * trans_p[y0][y] * emit_p[y][obs[t]], y0) for y0 in states) V[t][y] = prob newpath[y] = path[state] + [y] # Don't need to remember the old paths path = newpath n = 0 # if only one element is observed max is sought in the initialization values if len(obs) != 1: n = t print_dptable(V) (prob, state) = max((V[n][y], y) for y in states) return (prob, path[state]) # Don't study this, it just prints a table of the steps.def print_dptable(V): s = " " + " ".join(("%7d" % i) for i in range(len(V))) + "\n" for y in V[0]: s += "%.5s: " % y s += " ".join("%.7s" % ("%f" % v[y]) for v in V) s += "\n" print(s)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
| def viterbi(obs,
states,
start_p,
trans_p,
emit_p):
V
=
[{}]
path
=
{}
# Initialize base cases (t == 0)
for
y
in
states:
V[0][y]
=
start_p[y]
*
emit_p[y][obs[0]]
path[y]
=
[y]
# Run Viterbi for t > 0
for
t
in
range(1,
len(obs)):
V.append({})
newpath
=
{}
for
y
in
states:
(prob,
state)
=
max((V[t-1][y0]
*
trans_p[y0][y]
*
emit_p[y][obs[t]],
y0)
for
y0 in
states)
V[t][y]
=
prob
newpath[y]
=
path[state]
+
[y]
# Don't need to remember the old paths
path
=
newpath
n
=
0
# if only one element is observed max is sought in the initialization values
if
len(obs)
!=
1:
n
=
t
print_dptable(V)
(prob,
state)
=
max((V[n][y],
y)
for
y
in
states)
return
(prob,
path[state])
# Don't study this, it just prints a table of the steps.
def print_dptable(V):
s
=
" "
+
" ".join(("%7d"
%
i)
for
i
in
range(len(V)))
+
"\n"
for
y
in
V[0]:
s
+=
"%.5s: "
%
y
s
+=
" ".join("%.7s"
%
("%f"
%
v[y])
for
v
in
V)
s
+=
"\n"
print(s)
|
viterbi函数有如下参数: obs 是观察值序列,例如[‘normal’, ‘cold’, ‘dizzy’]; states是隐含的状态;start_p是初始概率;trans_p是转移概率;emit_p是发射概率(生成概率)。为了代码的简介性,我们假设obs是非空的并且trans_p[j]和emit_p[j]对所有的状态i,j都有值。
运行上述函数的代码如下:
<span class="kw1">def</span> example<span class="br0">(</span><span class="br0">)</span>: <span class="kw1">return</span> viterbi<span class="br0">(</span>observations<span class="sy0">,</span> states<span class="sy0">,</span> start_probability<span class="sy0">,</span> transition_probability<span class="sy0">,</span> emission_probability<span class="br0">)</span><span class="kw1">print</span><span class="br0">(</span>example<span class="br0">(</span><span class="br0">)</span><span class="br0">)</span>
1
2
3
4
5
6
7
| <span class="kw1">def</span>
example<span class="br0">(</span><span class="br0">)</span>:
<span class="kw1">return</span>
viterbi<span class="br0">(</span>observations<span class="sy0">,</span>
states<span class="sy0">,</span>
start_probability<span class="sy0">,</span>
transition_probability<span class="sy0">,</span>
emission_probability<span class="br0">)</span>
<span class="kw1">print</span><span class="br0">(</span>example<span class="br0">(</span><span class="br0">)</span><span class="br0">)</span>
|
程序显示最可能产生观察值[‘normal’, ‘cold’, dizzy’]的状态是[‘Healthy’, ‘Healthy’, ‘Fever’].也就是说,给定观察到的活动,病人最可能在第一天和第二天都是Healthy的,她第一天感觉正常第二天感觉冷,第三天的时候就确定开始发热了。
维特比算法的操作可以通过篱笆网络图 trellis diagram来可视化。维特比路径本质上就是通过篱笆网络的最短路径。诊所的例子对应的篱笆网络如下;对应的维特比路径被加粗显示。(注,Day3第一帧右下角的概率应该是P(‘dizzy’|newstat))
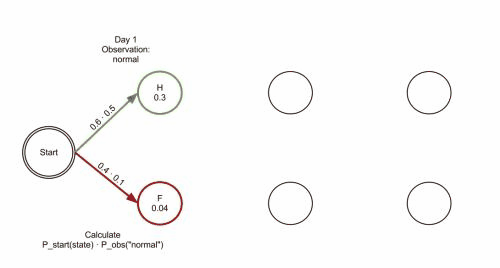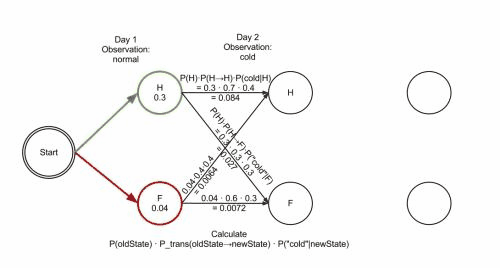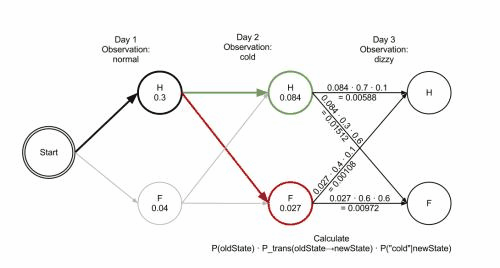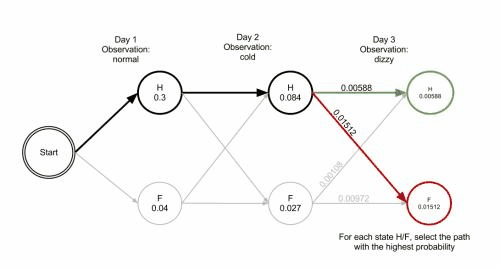
当实现维特比算法的时候,需要注意的是很多语言使用浮点运算,由于p很小,这会导致运算结果的溢出(underflow)。避免这个问题的常用技术是使用概率的对数运算(logarithm of the probabilities )。一旦算法运行完毕,可以通过合适的指数运算来取得概率的准确值。
扩展(Extensions)有一种维特比算法的泛化算法称为max-sum algorithm(也叫max-product algorithm), 在大量图模型(例如贝叶斯网络(Bayesian networks), 马尔科夫随机场(Markov random fields) 和 条件随机场( conditional random fields )). )中,该算法可用于寻找全部或者部分隐含变量( latent variables )的值。
使用迭代维特比解码(iterative Viterbi decoding)算法,对于给定的HMM我们可以找到观察值子序列的最佳匹配。
另外一种算法是最近提出的Lazy Viterbi algorithm,该算法在实践中比原来的维特比算法有更好的性能,因为该算只在实际需要的时候才进行节点扩展。
伪代码(Pseudocode)给定观察值空间O = {o1, o2, …, oN};状态空间S = {s1, s2, …, sK}, 观察值序列Y={y1, y2, …, yT};转移矩阵A(K×K), 其中Aij存储状态si到状态sj的转移概率;生成矩阵B(K×N), 其中Bij存储从状态si生成观察值oj的概率;大小为K的初始概率数组π, 其中πi存储x1 = Si的概率。设X = {x1, x2, …, xT}是生成观察值Y={y1, y2, …, yT}的状态序列。
在这个动态规划问题中,我们构造两个二维表T1, T2(大小均为K×T)。T1 的元存概率,T2的元素存路径。基于上述定义的伪代码 |
|


