10. 相关系数 ( Correlation coefficient )与相关距离(Correlation distance)
(1) 相关系数的定义
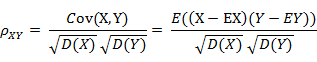
相关系数是衡量随机变量X与Y相关程度的一种方法，相关系数的取值范围是[-1,1]。相关系数的绝对值越大，则表明X与Y相关度越高。当X与Y线性相关时，相关系数取值为1（正线性相关）或-1（负线性相关）。
(2)相关距离的定义
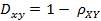
(3)Matlab计算(1, 2 ,3 ,4 )与( 3 ,8 ,7 ,6 )之间的相关系数与相关距离
X = [1 2 3 4 ; 3 8 7 6]
C = corrcoef( X' ) %将返回相关系数矩阵
D = pdist( X , 'correlation')
结果：
C = 1.0000 0.4781
0.4781 1.0000
D = 0.5219
其中0.4781就是相关系数，0.5219是相关距离。
11. 信息熵(Information Entropy)
信息熵并不属于一种相似性度量。信息熵是衡量分布的混乱程度或分散程度的一种度量。分布越分散(或者说分布越平均)，信息熵就越大。分布越有序（或者说分布越集中），信息熵就越小。
计算给定的样本集X的信息熵的公式：
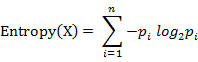
参数的含义：
n：样本集X的分类数
pi：X中第i类元素出现的概率
信息熵越大表明样本集S分类越分散，信息熵越小则表明样本集X分类越集中。。当S中n个分类出现的概率一样大时（都是1/n），信息熵取最大值log2(n)。当X只有一个分类时，信息熵取最小值0
参考资料：
[1]吴军. 数学之美 系列 12 – 余弦定理和新闻的分类.
http://www.google.com.hk/ggblog/googlechinablog/2006/07/12_4010.html
[2] Wikipedia. Jaccard index.
http://en.wikipedia.org/wiki/Jaccard_index
[3] Wikipedia. Hamming distance
http://en.wikipedia.org/wiki/Hamming_distance
[4] 求马氏距离（Mahalanobis distance ）matlab版
http://junjun0595.blog.163.com/blog/static/969561420100633351210/
[5] Pearson product-moment correlation coefficient
http://en.wikipedia.org/wiki/Pearson_product-moment_correlation_coefficient
转载自：http://goo.gl/zRXbt
此条目由 lixiang 发表在 Machine Learning 分类目录，并贴了 Chebyshev Distance、Cosine、Euclidean Distance、Hamming Distance、Information Entropy、Jaccard Distance、Mahalanobis Distance、Manhattan Distance、Minkowski Distance 标签。将固定链接加入收藏夹。
欧氏距离与余弦相似度
欧氏距离是最常见的距离度量，而余弦相似度则是最常见的相似度度量，很多的距离度量和相似度度量都是基于这两者的变形和衍生，所以下面重点比较下两者在衡量个体差异时实现方式和应用环境上的区别。
借助三维坐标系来看下欧氏距离和余弦相似度的区别：
从图上可以看出距离度量衡量的是空间各点间的绝对距离，跟各个点所在的位置坐标（即个体特征维度的数值）直接相关；而余弦相似度衡量的是空间向量的夹角，更加的是体现在方向上的差异，而不是位置。如果保持A点的位置不变，B点朝原方向远离坐标轴原点，那么这个时候余弦相似度cosθ是保持不变的，因为夹角不变，而A、B两点的距离显然在发生改变，这就是欧氏距离和余弦相似度的不同之处。
根据欧氏距离和余弦相似度各自的计算方式和衡量特征，分别适用于不同的数据分析模型：欧氏距离能够体现个体数值特征的绝对差异，所以更多的用于需要从维度的数值大小中体现差异的分析，如使用用户行为指标分析用户价值的相似度或差异；而余弦相似度更多的是从方向上区分差异，而对绝对的数值不敏感，更多的用于使用用户对内容评分来区分用户兴趣的相似度和差异，同时修正了用户间可能存在的度量标准不统一的问题（因为余弦相似度对绝对数值不敏感）。
上面都是对距离度量和相似度度量的一些整理和汇总，在现实的使用中选择合适的距离度量或相似度度量可以完成很多的数据分析和数据挖掘的建模，后续会有相关的介绍
补充：编辑距离；K-L divergence
.
12 hausdorff距离 微分动力系统原理这本书里有介绍 Hausdorff距离是描述两组点集之间相似程度的一种量度，它是两个点集之间距离的一种定义形式：假设有两组集合A={a1,…,ap},B={b1,…,bq},则这两个点集合之间的Hausdorff距离定义为H(A,B)=max(h(A,B),h(B,A)) (1) 其中, h(A,B)=max（a∈A）min（b∈B）‖a-b‖ (2) h(B,A)=max（b∈B）min（a∈A）‖b-a‖ (3) ‖·‖ 是点集A和B点集间的距离范式(如 2或Euclidean距离). 这里,式(1)称为双向Hausdorff距离,是Hausdorff距离的最基本形式;式(2)中的h(A,B)和h(B,A)分别称为从A集合到B集合和从B集合到A集合的单向Hausdorff距离.即h(A,B)实际上首先对点集A中的每个点ai到距离此点ai最近的B集合中点bj之间的距离‖ai-bj‖进行排序,然后取该距离中的最大值作为h(A,B)的值.h(B,A)同理可得. 由式(1)知,双向Hausdorff距离H(A,B)是单向距离h(A,B)和h(B,A)两者中的较大者,它度量了两个点集间的最大不匹配程度. |
