插入、合并、堆、快速排序通过对数组中的元素进行比较来实现,对任何n个输入来说,最坏运行时间下界为Ω(n*lgn)。
注:lgn是log2(n)
A是一个任意数组,这里举例为A[10] = {16,14,10,8,7,9,3,2,4,1}
将数组以二叉树形式展示,结点下标与数组下标对应:
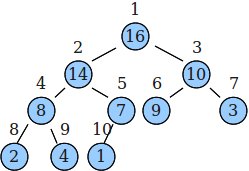
i的父节点parent(i) = i/2
左节点left(i) = 2i
右节点right(i) = 2i + 1
1.将一个以i为根的子树转换为子最大堆
最大堆是满足下列条件的完全二叉树:除了根以外的每个节点i,都有A[parent(i)] >= A
转换过程:
MAX-HEAPIFY(A,i)
{
l = left(i)
r = right(i)
heap-size[A] = lenght(A)
if l <= heap-size[A] && a[l] > a
{
then largest = l
else largest = i
}
if r <= heap-size[A] && a[r] > a[largest]
{ then largest = r}
if i != largest
{
then exchange( a, a[largest] )
MAX-HEAPIFY(A,largest)
}
}
运行时间为O(lgn)
2.创建最大堆
一棵n个元素组成的二叉树中,元素A[n/2 + 1], A[n/2 + 2],...,A[n]都是树的叶子,因此每个都可以看成是只有一个元素的堆而无需转换成最大堆
建堆过程:
BUILD-MAX-HEAPIFY(A)
heap-size[A] = lenght(A)
for (i = heap-size[A]/2; i >= 1; i--)
{
MAX-HEAPIFY(A,i)
}
初步分析每次调用MAX-HEAPIFY(A,i)所用的时间为O(lgn),一共调用了O(n)次,故该算法运行时间为O(n*lgn);实际上,在树中不同高度的结点处运行MAX-HEAPIFY的时间不同,大部分结点的高度都较小。一个n元素堆的高度为lgn,在任意高度上,最多有n/2^(h + 1)个结点,故BUILD-MAX-HEAPIFY更准确的运行时间为:O(n)
3.排序
HEAPSOTR(A)
BUILD-MAX-HEAPIFY(A)
for (i = length(A); i >= 2; i--)
{
exchange(A, A[1])
MAX-HEAPIFY(A,1)
heap-size[A] = heap-size[A] -1
}
HEAPSOTR过程的时间代价为O(n*lgn),其中BUILD-MAX-HEAPIFY的时间代价为O(n),n-1次MAX-HEAPIFY的时间代价为O(lgn)
代码实现:
/*
*name: max_heap.c
*author: ls
*date: 2012-04-26
*destribution: 堆排序实现
*/
#include <stdio.h>
//创建最大树子树
void max_heapify(int array[], int len, int i)
{
int left,right;
int largest;
int tmp;
left = 2 * i + 1;
right = 2 * i + 2;
int main()
{
int i, tmp;
int len = 12;
int array[12] = {11, 3, 6, 4, 9, 12, 2, 7, 8, 5, 10, 1};
create_max_heapify(array, len);
for (i = len - 1; i >= 1; i--)
{
tmp = array;
array = array[0];
array[0] = tmp;
len--;
max_heapify(array, len, 0);
}
for (i = 0; i < 12; i++)
{
printf("%d ", array);
}
printf("\n");
return 0;
} |